如何显示HDR

（注：本人对显示器技术了解有限，这一部分可能不够准确。另外，国内外网络上关于这些东西的说明实在太少，结合了我的一些个人理解，我尽量做到不自我矛盾）

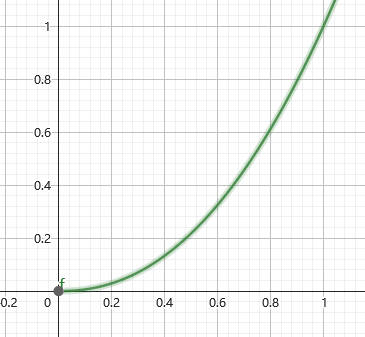
白色\([255,255,255]\)、红色\([255,0,0]\)这样的颜色是怎么显示在屏幕上的呢？首先，将其转化为标准化的\([1.0, 1.0, 1.0]\)、\([1.0, 0.0, 0.0]\)，然后发送到显示器，显示器中分别显示RGB三种颜色的灯泡就会按照这个值去发出特定的亮度，这个特定的亮度由电光转换（EOTF）函数决定，在SDR显示器中，这个函数通常是gamma传递函数

\[Y = E^\gamma \]

这里\(E\)是我们给予的颜色值\([0, 1]\)，而\(Y\)是标准化的亮度值\([0,1]\)，其中\(0\)代表灯泡的最低亮度，而\(1\)代表灯泡的最高亮度。\(\gamma\)就是我们说的gamma值，一般会取\(2.2\)。一般来说，SDR显示器的最高亮度定义为\(100\)nits，所以

\[F_D = 100Y = 100E^\gamma \]

其中\(F_D\)是显示器理论上会发出的亮度值。

HDR的含义是高动态范围，要求我们能够显示更高的亮度，即超越\(100\)nits达到\(400\)、\(1000\)甚至更高的nits。虽然理论上来说你确实可以将\(F_D = 400Y\)来适应更高的亮度，但是使用其他曲线能够更好的符合人眼感知特性（以及其他原因，见后）。特别的，在HDR领域用的最多的是PQ曲线和HLG曲线，这里我们主要讲PQ：

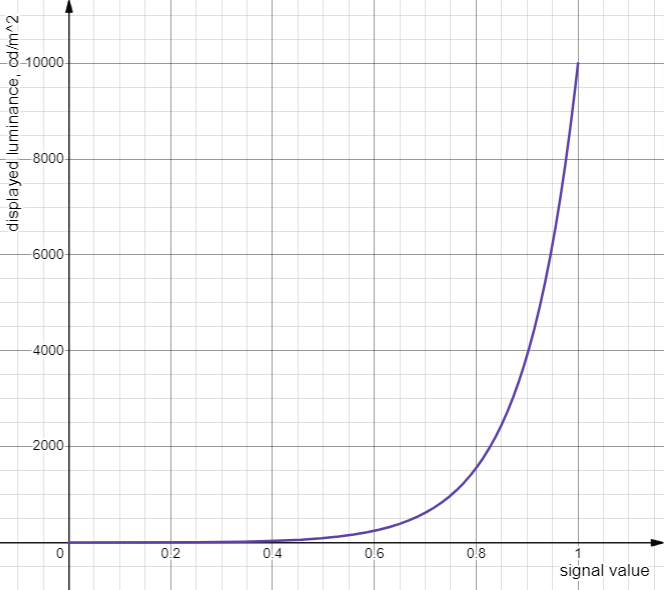
\[F_D = 10000\left(\dfrac{\max[(E^{1/m_2}-c_1),0]}{c_2-c_3\cdot E^{1/m_2}}\right)^{1/m_1} \]

具体的参数数值可以在https://en.wikipedia.org/wiki/Perceptual_quantizer找到。由公式和图像可知，PQ曲线最高支持到10000nits亮度。

PQ曲线是同样的，那对于只有400nits亮度的显示屏如何显示1.0大小的信号呢？答案是：不要使用1.0大小的信号。通过某一些方法（见后，即tonemapping）将1.0大小的信号缩放到0.7左右，并且视频、图像文件里都只存0.7以下的数字。

实际上这并不是乱说的，HDR视频制作过程中metadata确实会有记录视频制作时的显示器亮度，以及视频播放时显示器的亮度（至少HDR Vivid确实有），这对于HDR的合理播放至关重要。

当然，这是假设了一个显示器直接根据PQ值输出亮度，实际上有些显示器自带tone mapping将PQ曲线规定的0~10000nits映射到自己的亮度值如0~400nits。据说也有的显示器是直接将超出的亮度裁剪掉。

接下来我们再来说说位深。从刚刚的描述中你也注意到，我们完全可以用\([0,255]\)来表示HDR的所有亮度值\([0,1]\)啊，为什么我们经常说HDR必须用上\(10\)bit呢？

我们先以简单的线性视角来看，如果要量化\([0,100]\)nits这个区间，我们使用\(8\)位深度，那么就是用\(256\)个数去表示\([0,100]\)，每两个连续的量化之间的差异是\(100/256\approx 0.4\)。而如果我们要量化\([0,10000]\)nits这个区间，那么差异就是\(10000/256\approx40\)，大了一百倍，这造成的结果就是渐变变化跨度太大，有“条带”现象的出现。举个例子如下，从左到右量化精度越来越高，两个连续量化之间的差异越来越小。

问题是10bit用来量化10000nits他仍然有\(10000/1024\approx 10\)的连续差异啊？为什么HDR显示器10bit甚至8抖10bit就可以满足要求？这时我们就要脱离出线性的视角，实际上，在PQ域里，100nits对应的信号值是\(0.5081\)，而10000nits对应的是\(1.0\)。这就意味着我们使用10bit位深，来量化\([0,1.0]\)这个区间，虽然\([0,511]\)负责量化\([0,0.5]\)，而\([512, 1023]\)负责量化\([0.5, 1.0]\)，但是将其使用PQ曲线转化后，实际上\([0, 511]\)量化了\([0, 100]\)nits，而\([512, 1023]\)量化了\([100, 10000]\)nits。换句话说，亮度越低的地方量化误差越小。

根据https://en.wikipedia.org/wiki/High-dynamic-range_television#Transfer_function所说，想要避免条带问题，在PQ域量化完整的10000nits需要至少12bits。而我们一般的HDR显示器也就支持到400nits，好一点的1000nits，用10bit来量化这些亮度低的地方完全足够。

回到之前的问题，为什么不再用gamma曲线了呢？除了人眼感知的一些因素，还因为gamma域中的10000nits量化要避免条带问题，至少需要15bit的位深。所以说白了，其实传递函数是对于量化亮度的分配规则（虽然gamma最初来源于CRT显示器的物理特性），将人眼最敏感的那部分区域用最多的空间去表示，而其他不敏感的地方用较少的空间区表示。

接下来还有颜色空间的问题。HDR10这样的标准确实规定了颜色空间必须是Rec2020，但是从上面的介绍中你也认识到，要显示HDR和颜色空间没有什么关系，你就算只支持灰度显示也可以HDR。不过，你若想将HDR映射到SDR显示器上显示，你仍然需要在tonemapping过后将Rec2020转到Rec709，防止SDR显示器显示有偏差的颜色。

Tone Mapping的作用

最初是没有HDR显示器的，Tone mapping的作用是将用各种技术捕捉到的具有高亮度的图像，恰当的显示在SDR显示器上。通常来说，一张照片中的很大部分内容都在\([0,100]\)nits之间，可以被SDR显示器正常显示，而只有很少一部分（例如太阳直射），具有很高的亮度，比如1000nits。而Tone mapping要做的事是，保留大部分正常显示的内容亮度不降低太少，而大幅度降低过于亮的部分。例如，我们可以用\([0,80]\)nits来显示原来\([0,100]\)的内容，而使用\([80, 100]\)nits显示所有大于100nits的内容。实际上，HDR显示器的最高亮度也各不相通，如何将适配于HDR1000的视频映射到HDR400也是Tone Mapping需要做的事。

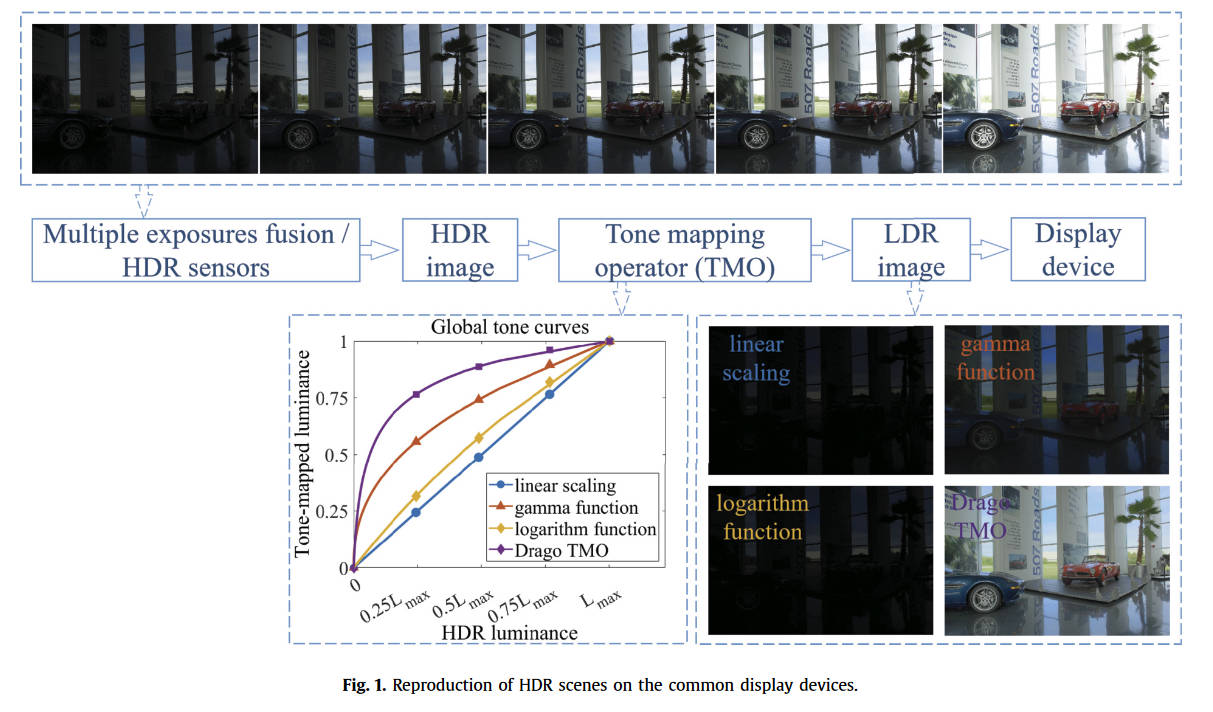
你可能会说这和刚刚提到的EOTF很像，都是在限定的范围内合理分配数值。那我们可不可以直接将PQ域的数据转换到线性域，再从线性域转换到Gamma域呢？答案是可以，但是不够好。借用论文High Dynamic Range Image Tone Mapping: Literature review and performance benchmark中的一张图（本文之后的内容也会极大程度参考该综述）

使用不同的Tone mapping效果是不一样的。上面的gamma曲线的图像明显是不如Drago曲线的，也就是说，gamma曲线对于HDR源的压缩还不够好，因为它毕竟只是为了SDR源而设计的。

在不同地方，Tone mapping曲线的目标可能是不一样的。例如在图形渲染当中，为了符合更好的物理规律，镜面反射+漫反射+环境光的亮度可能会大于1.0，这里的Tone mapping目的在于将\([0, +\infty]\)的亮度映射到\([0, 1]\)之间，然后再去gamma校正。而对于HDR Vivid这样的视频处理，其规则为：PQ域-线性域-Tone mapping-Gamma域，首先转化为\([0,1]\)之间的标准化亮度，然后Tone mapping负责将这个\([0,1]\)映射到另一个\([0,1]\)上，更符合Gamma域的颜色分布，然后进行伽马校正。

通常，Tone mapping是在“亮度”上进行的，而非分别在RGB上做（当然也有），在改变亮度后再进行“颜色恢复”，形式如下

\[C' = \left(\dfrac{C}{L}\right)^s T \]

其中，\(C\)是指原图中某个像素的RGB通道中的任意一个的数值，而\(C'\)则是其对应的Tone mapping后的结果数值。\(L\)是该像素的亮度，而\(T\)是\(L\)使用Tone mapping曲线计算出来的结果，\(s\)是颜色补偿参数，一般会取\(1\)，如果小于\(1\)就会欠饱和。所以，面向亮度进行的Tone mapping就是在研究如何将\(L\)转换成\(T\)。

首先先谈一谈如何计算某个像素的亮度值。这通常很经验，要么就是根据某种人眼的生物学研究，但是有几个形式用的比较多，最多的可能是：

\[L = 0.2959R + 0.5870G + 0.1140B \]

即RGB的加权平均（事实上，人眼确实对绿色的亮度最敏感）。而像HDR Vivid这样的体系会使用\(L=\max\{R,G,B\}\)。虽然没有确切证据证据，但是前者恰好是RGB转YUV中Y的定义，而后者正好是RGB转HSV中V的定义。

只考虑单个像素亮度的TMO

（注：TMO是Tone Mapping Operator）

如果我们整张图只用一根曲线，并且只考虑某个像素自己的信息，那么这也可以叫做Global TMO。

例如，极简化的Reinhard方法可以被写作

\[T = \dfrac{L}{1+L} \]

其将\([0,+\infty]\)映射到\([0, 1]\)上。更多的这种用在游戏领域的GTMO可以看https://zhuanlan.zhihu.com/p/21983679，它们的显著特点就是形式简单，速度超快。（另外他这里面全是RGB上直接做的，而Reinhard的原论文取的是\(L=0.27R+0.67G+0.06B\)）

这样的单根曲线很多时候是根据人眼视觉系统（human visual system, HVS）的特性来设计的，例如论文Adaptive logarithmic mapping for displaying high contrast scenes中，就使用了

\[L_d = \dfrac{L_{dmax}\cdot 0.01}{\log_{10}(L_{wmax}+1)}\cdot\dfrac{\log(L_w+1)}{\log\left(2+\left(\left(\dfrac{L_w}{L_{wmax}}\right)^{\dfrac{\log(b)}{\log(0.5)}}\right)\cdot 8\right)} \]

这样的公式，这里的\(L_w\)就是映射前的亮度，\(L_d\)就是映射后的亮度，而\(L_{dmax}\)一般取100代表显示器的最大亮度，\(b\)是可调参数。

还有一种方法是根据直方图来的，例如Tone-mapping High Dynamic Range Images by Novel Histogram Adjustment可以被极简化的写作

\[D(I) = (D_{max}-D_{min})\times \dfrac{\log(I+\tau)-\log(I_{min}+\tau)}{\log(I_{max}+\tau)-\log(I_{min}+\tau)}+D_{min} \]

其中\(D_{max}, D_{min}\)是显示器的最大最小亮度，而\(I_{max}, I_{min}\)是场景中的最大最小亮度。（注：曲线对于同一张图片是固定的，不同位置的像素拥有相同的输入就有相同的输出）

也有研究者引入了聚类算法，对不同的类别进行统计，决定该图像的映射曲线使用什么参数。

这类GTMO的问题在于，其对于局部对比度的保护不好。尤其是在特别亮和特别暗的地方，这些曲线倾向于将它们映射到非常接近的亮度，而一个像素和其周围的像素亮度通常是接近的，使用GTMO就丢失了局部对比度。

考虑周围像素亮度值的TMO

为了解决局部对比度的问题，Local TMO就被提出了。GTMO理论上同一张图片里相同的亮度会被映射成相同的结果，但LTMO就允许映射成不同的结果，来保护局部的对比度。

考虑空间上的信息的研究中比较著名的是完全体版Reinhard，在传统的摄影技法中，摄影师能够通过调整曝光时间来将结果中的暗的地方增亮，亮的地方变暗，从而让结果包含更多有效信息。Reinhard方法通过自动的方法来进行这种操作（实际上是反向操作）。作者使用高斯滤波器来找到这种局部亮度差不多的像素，然后通过减被亮像素包围的暗像素，提亮被暗像素包围的亮像素，于是就成功的将局部的对比度提高了。

\[V(x,y,s) = \dfrac{V_1(x,y,s)-V_2(x,y,s)}{2^\phi a/s^2+V_1(x,y,s)} \]

这里的公式里的\(V_i\)就是高斯滤波后的结果，其中\(s\)控制了方差大小，\(a,\phi\)是可调参数。\(V_1, V_2\)的区别在于其方差被乘以了一个不同的常数，\(V_1\)乘以了比较小的数，而\(V_2\)乘以了比较大的数。

在图片中\(V_1\)和\(V_2\)在亮度梯度小的地方数值差距小，在亮度梯度大，也就是局部对比度大的地方数值差距大。作者通过搜索\(s\)的方法，来让这整个式子的绝对值第一次小于一个限定值。通过这样的方式就可以寻找到一个local区域，其用\(s_m\)来表示这个区域的大小。

分母上的\(V_1\)来让这个式子和亮度绝对值无关，而\(2^\phi a/s^2\)则可以防止\(V\)变成极端值。计算完最优的\(s_m\)后，这里的\(V_1\)就可以用来表示该像素的局部平均值，于是我们就可以修改之前的极简版Reinhard为：

\[L_d(x,y) = \dfrac{L(x,y)}{1+V_1(x,y,s_m(x,y))} \]

当遇到亮区域的暗像素时，就有\(L< V_1\)，于是\(L_d\)就会更小，即让差不多亮的地方的暗的地方更暗一点，反之则让亮的地方更亮一点，从而增加了局部的对比度。

而在频域的信息上来做的最著名的是Durand & Dorsey方法，原文大篇幅在讲滤波，我看不懂，但是其LTMO的思路如下（参考自https://zhuanlan.zhihu.com/p/573894977）

通过我们之前加权求和方法计算图片的亮度图，并且将其进行对数运算，得到对数域亮度图\(L\)
在\(L\)上进行双边滤波，得到\(B\)，即代表了基础层，我们需要压缩这部分
计算细节信息层（局部对比度就在这里）\(D=L-B\)
以某种方法压缩\(B\)，例如直接乘以常数，或者使用某种GTMO（我试过真的可以，不过要先从对数域转换回去，之后再转换回来），得到压缩后的结果\(B'\)
重新算出全图亮度\(L'=B'+D+\beta\)，这里的\(\beta\)是曝光补偿参数，可调。
将\(L'\)从对数域转回去，得到了新的亮度，然后使用我们之前说的颜色恢复方法恢复回去就可以了。

当然，这里的细节层也不是不可以增强或者压缩，看自己的选择。这种方法的原理是利用了双边滤波的特性，其可以保护边缘信息，而将其他变化平缓的部分取均值，从而我们可以通过计算出基础层\(B\)，然后用用\(L-B\)得到细节层\(D\)。实际上这个\(D\)就是将原图中的边缘信息去除，然后留下平缓部分的“差异”，也就是“局部对比度”。

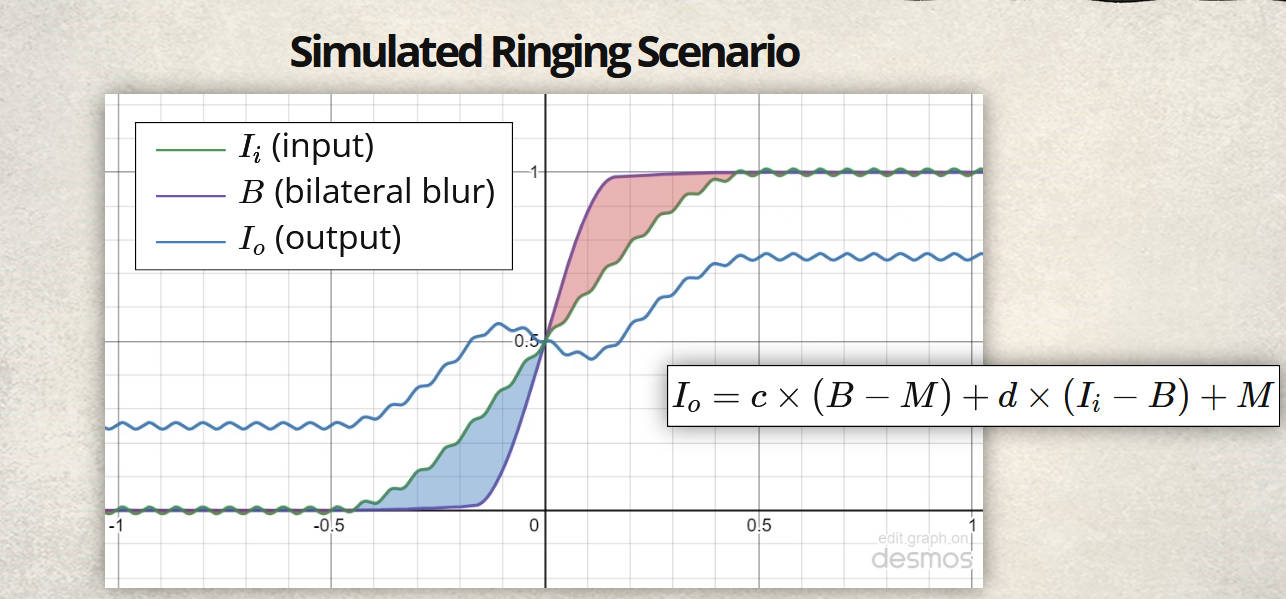
之前用双边滤波可能会有点性能问题，但是双边网格被发明后，再加上现在电脑的算力提升，这种方法也是逐渐可以用到游戏里了，例如对马岛之魂中，就应用了这种技术，其算法我认为本质上和上文的是相同的：

\[I_o=c\times (B-M) + d\times (I_i-B) + M \]

上面这些全在对数域，\(I_o, I_i\)就是输出和输入亮度，\(B\)是滤波得到的基础层，\(M\)是亮度的中值。\(c\)是调整对比度的可调参数，\(d\)是调整细节的参数。

双边滤波的问题是会有光晕问题。作者给出的解释如下

我认为作者的意思是想说，在减少对比度的同时，增加细节，就会让这根曲线从“大体上单增”，变成了一个“大体上先增后减再增“的曲线，正是这种奇怪的过渡使得光晕产生。或者用“梯度反转”这个词来表示，也就是说，原来亮度高的地方变成了亮度低的，而亮度低的变得亮度高了，体现出来就是围绕着边缘处有一圈比边缘内更亮的区域，即“光晕”。

而作者给出的解决办法就是混合使用高斯滤波和双边滤波。大概40%的双边，60%的高斯，而且高斯核必须足够大。

考虑像素颜色值的TMO

我们之前说的颜色恢复并不是那么准确，像那样改亮度实际上是会稍微影响到色度的。

TODO

深度学习的TMO

基于GAN的监督学习方法

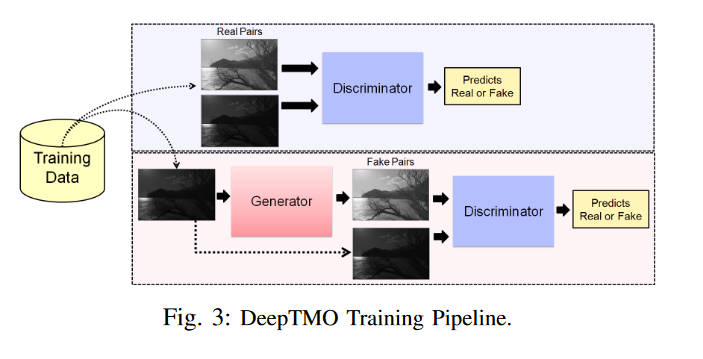
例如论文Deep tone mapping operator for high dynamic range images提出的DeepTMO，其使用cGAN的架构来对给出的HDR图片进行LDR图片的生成

如图，其从训练数据中拿出HDR和其对应的真实LDR图片的亮度图给判别器，让其判断LDR是否是从HDR中生成的。而生成器的任务就是从HDR亮度图中生成假的LDR亮度图，然后尽可能让判别器判断不出来。

训练数据是作者实现了一系列经典的TMO，然后用他们将HDR图片数据集转化为LDR图片，使用客观评价标准Tone Mapped Image Quality Index (TMQI)来判断表现最好的LDR，然后将其作为真实LDR标注图片。

本文的想法是之前的TMO对不同场景的表现不同，在高亮度表现好的TMO不一定在低亮度表现好，或者这些TMO需要调整参数才能适应不同的场景。本文提出的DeepTMO希望免去输入参数的步骤，直接进行场景的自适应，对不同条件的光照都生成最好的结果。

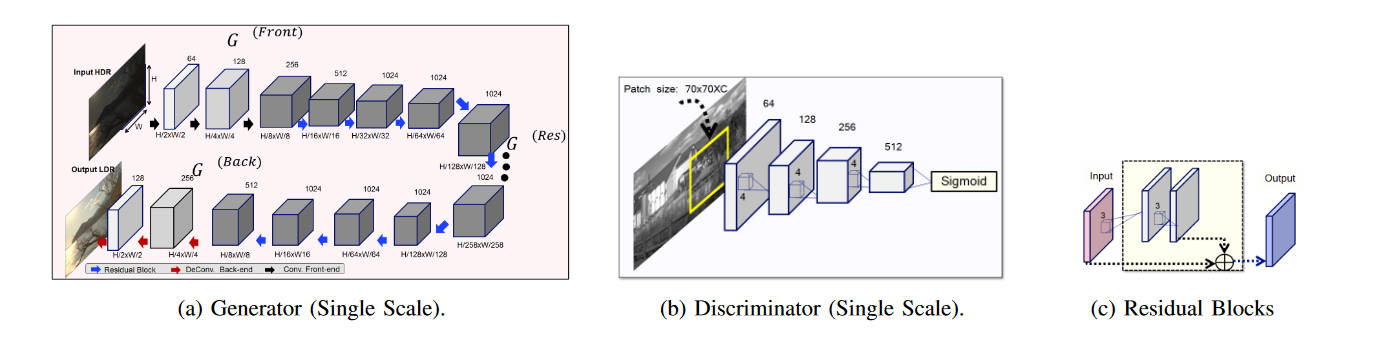
其单尺度的网络结构如下

生成器是一个卷积、残差块、反卷积的编解码器结构，输入HDR亮度图输出同分辨率的LDR亮度图。而判别器的架构是PatchGAN，每次只对一个\(70\times 70\)的空间进行判断，最终再将所有Patch的判断综合起来进行全图的判断。用PatchGAN的好处，作者认为是参数少，并且可以应用到任意大小的图片上。

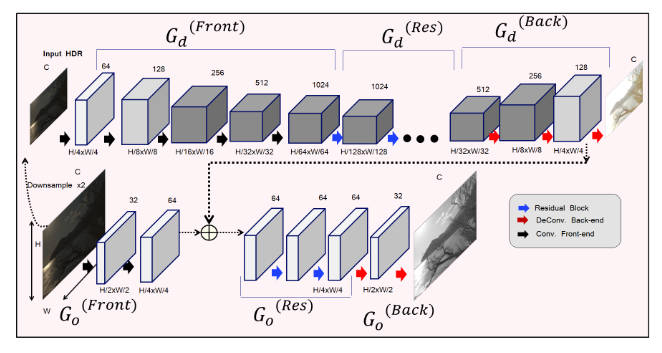
然而单尺度的DeepTMO还是太弱了，有细节处的伪影，所以作者又提出了多尺度的加强版。

作者这里只给出了生成器的结构。上图所示的两个生成器\(G_d,G_o\)都和原来的架构是一样的，\(G_d\)接收下采样过两次的输入。\(G_o\)负责进行局部细节的Tone mapping，而\(G_d\)负责进行整体的、粗糙的。判别器没给图，结构和之前一样，只不过\(D_d\)负责判断全局的真假，而\(D_o\)负责局部细节的。同样的\(D_d\)的输入是经过两次下采样的图片。

基于GAN的半监督学习方法

实际上，先用一些传统TMO得到LDR，再选出指标最好的一个，也不能避免传统TMO的伪影问题。按理来说，使用摄影师手动调整过的图片是最好的，但是这样又太费时。

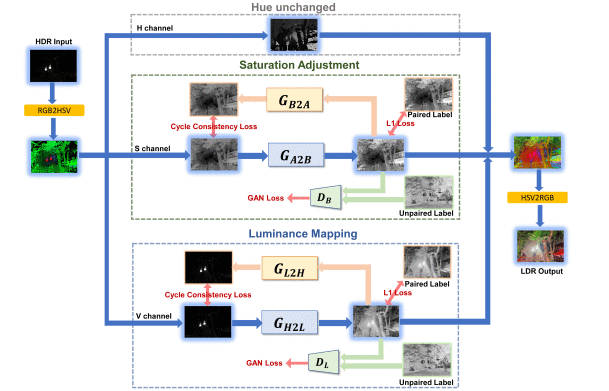
A Real-Time Semi-Supervised Deep Tone Mapping Network提出了一种半监督方法，文中指出了直接使用CycleGAN这样的无监督方法效果不好，需要加一点配对数据来提升能力。本文的网络结构如下

作者首先指出，RGB转化为HSV，并且分别处理亮度和饱和度是最好的。本文引入配对标注数据的方法是，在原有的CycleGAN的基础上加上一个配对数据的\(L_1\)损失，对于\(V\)通道

\[L_1 = E_{(h,l_p)}||G_{H2L}(h)-l_p||_1 \]

其中\(h\)指HDR图，\(l_p\)指其对应的人类专家编辑的LDR图标注。而对于\(S\)通道

\[L_1 = E_{(a,b_p)}||G_{A2B}(a)-b_p||_1 \]

形式一样。然后将这两个损失分别加到各自的CycleGAN之前有的那一堆损失里。遇到没有配对图片的情况，损失就取\(0\)。

关于生成器和判别器的网络架构，比较公式就略过了，重要的思想是前面的添加配对数据的部分。

基于DNN的无监督学习方法

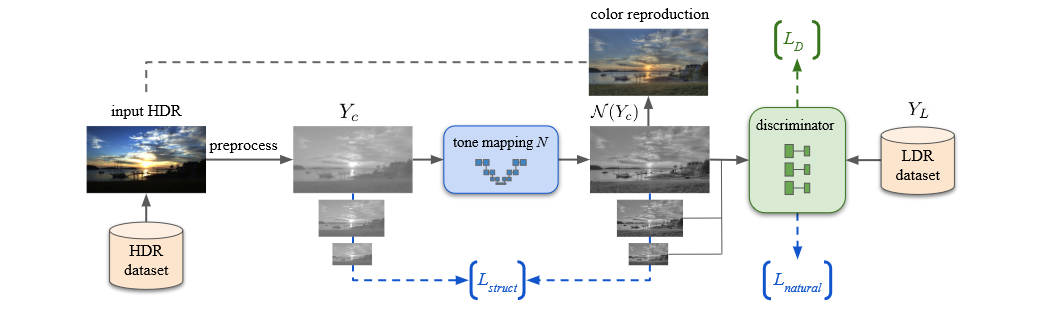
Unpaired learning for high dynamic range image tone mapping一文中介绍了一种无监督的方法，即不使用配对的HDR-LDR数据。网络结构如下

和大多数工作一样，本文仅在亮度上进行Tone mapping，之后再进行颜色恢复，特别的，使用RGB转YUV后的Y通道。本文并算不上GAN，虽然他确实有判别器，但是他并没有生成器。首先本文将\(Y\)通道应用一个log型的曲线进行动态范围压缩

\[Y_c(x)=\log\left(\lambda\dfrac{Y(x)}{\max(Y)}+\varepsilon\right)/\log(\lambda+\varepsilon) \]

其中\(\lambda\)是一个可调参数，而\(\varepsilon=0.05\)是一个常数。本文的网络\(N\)的作用是在\(Y_c\)上进行微调，以保证局部对比度，移除其他伪影。为了保证\(N\)输出的亮度特征和LDR的特征相似，本文引入了判别器，判断一个输入图片是否为LDR，另外，本文学习前人的工作使用了多尺度的判别器。即将真假的LDR的原图、下采样过1次、2次的图分别用三个判别器进行判别。判别器的误差如下

\[L_D = \sum_{k=\{0,1,2\}}\left(E_{Y_L\sim LDR}[D_k(\downarrow^kY_L)-1]^2+E_{Y\sim HDR}[D_k(\downarrow^kN(Y_c))]^2\right) \]

其中\(\downarrow^k\)指的是下采样过\(k\)次。这个判别器会给网络\(N\)传递一个误差，目的是让其亮度表现的像LDR

\[L_{natural} = \sum_{k=\{0,1,2\}}E_{Y\sim HDR}[D_k(\downarrow^kN(Y_c))-1]^2 \]

以上的部分只是让生成的LDR亮度看起来就像人类专家精心编辑过的LDR图片一样，但是他并没有要求假LDR图片拥有和原图一样的“结构”，也无法解决局部对比度等问题，所以：

\[L_{struct} = \sum_{k=\{0,1,2\}}\rho(\downarrow^kY_c,\downarrow^kN(Y_c)) \]

其中

\[\rho(I,J) = \dfrac{1}{n_p}\sum_{p_I, p_J}\dfrac{cov(p_I, p_J)}{\sigma(p_I)\sigma(p_J)} \]

是皮尔逊相关系数，其中\(p_I, p_J\)是两张图片上对应的\(5\times 5\)的小块。

最后是关于前面说的log型曲线的参数选择，使用数值算法求解最优值

\[\lambda = \text{argmin}-\sum_lH_l(Y_c)\log(H_l(LDR)) \]

其中\(H(Y_c)\)是\(Y_c\)的直方图，而\(H(LDR)\)则是数百张精挑细选过的LDR图片的直方图均值。直方图总共有\(20\)个bins。作者说只考虑HDR图片的亮度最大值最小值可能会受到噪声的干扰，效果不好。

基于扩散模型的无监督学习方法

如果说上面那个还要用HDR图片来训练的话，下面这个方法连HDR都不用了，干脆就是只用LDR训练，直接在HDR上推理。

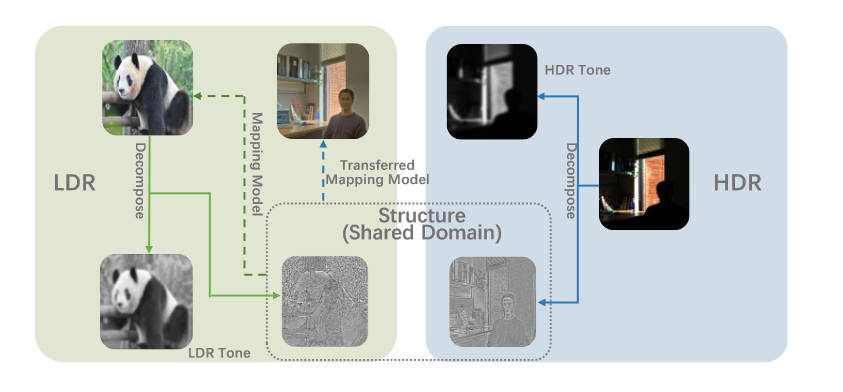
Zero-Shot Structure-Preserving Diffusion Model for High Dynamic Range Tone Mapping发现HDR和其LDR的结构是“几乎相同”的，细微的差别实际上是不完美的TMO造成的。本文使用的结构指标如下

\[\mu(i,j) = \sum^K_{x=-K}\sum^K_{y=-K} \omega(x,y)I(i+x, j+y) \]

\[\sigma(i,j) = \sqrt{\sum^K_{x=-K}\sum^K_{y=-K} \omega(x,y)[I(i+x, j+y)-\mu(i,j)]^2} \]

\[\hat I(i,j) = \dfrac{I(i,j)-\mu(i,j)}{\sigma(i,j)+\varepsilon} \]

其中\(\omega(x, y)\)是高斯核。最后这个公式就是结构指标，作者称之为MSCN，作者通过实验验证，在JS散度的意义上，LDR和HDR图片的结构分布是极为相似的，或者直接假设为同分布。于是，本文就通过这个结构上同分布的假设，在LDR和HDR上建立了知识迁移的桥梁。

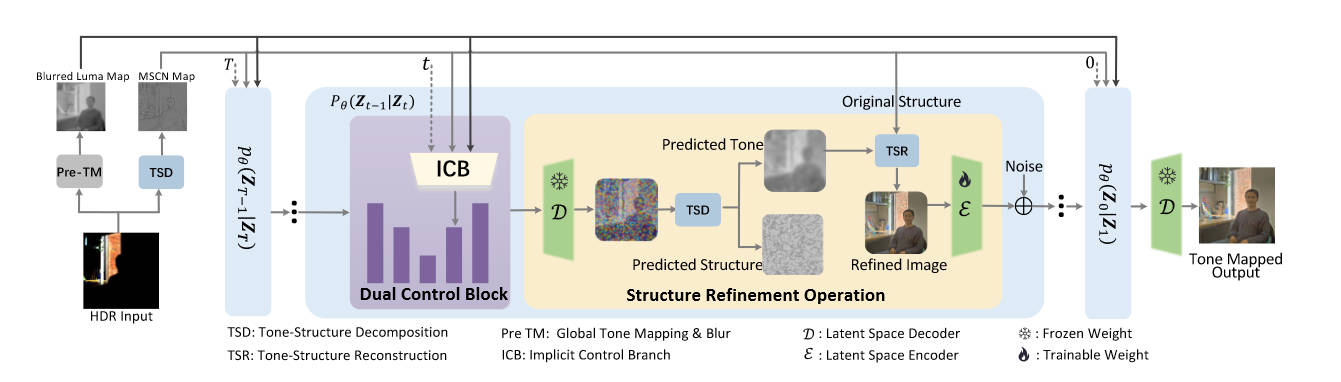
网络结构如下

大致的思想就是在ControlNet上进行，输入的控制条件是MSCN、以及经过高斯模糊后的亮度图。在训练过程中，使用LDR图片，提取到其MSCN，然后对其转为YUV通道后的Y进行高斯模糊，作为亮度图。输入到Control模块后，期望其能够复现出原始的LDR图片的亮度图。而在推理过程中，使用HDR图片，也是提取到其MSCN，然后像上一篇文章一样，用log型曲线先把YUV的Y压缩一下，再进行高斯模糊。然后也是把这两个图输入到Control模块，就得到了LDR图片的亮度图，后面再进行颜色恢复。

文中还提出了一个SRO的操作，在每一步diffusion之后，将其中间结果也分成Y通道和MSCN，然后将MSCN偷换成原图中提取的MSCN，然后将其和Y通道合并后得到一个结果，将这个结果发送给下一步diffusion的输入。

基于语义分割的方法

有一些方法试图对不同的区域应用不同的Tone mapping，因为关注到显然现实生活中不同材质的物体平均亮度是不同的，可以通过这种方式来将各种物体映射到各自偏好的亮度。

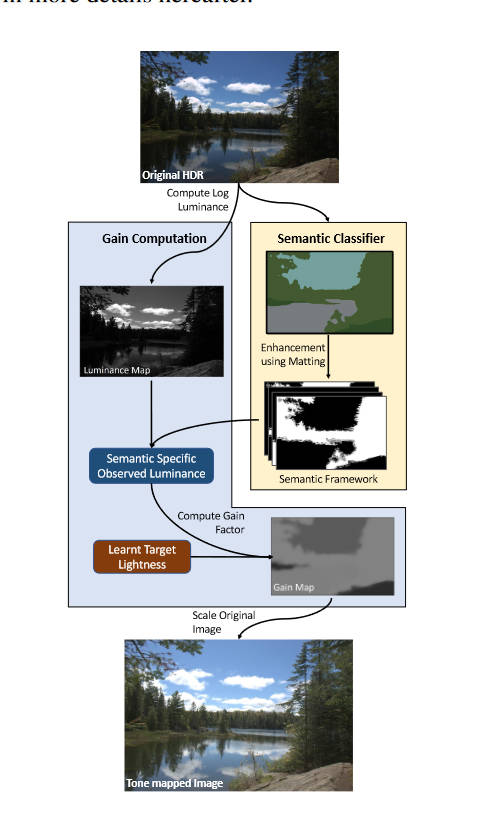
文章Tone Mapping Operators: Progressing Towards Semantic-Awareness的结构如下

本文并没有提出什么新的网络架构。Mask的提取部分，使用了预训练的FastFCN，将其中的150个类又归为9类，然后使用形态学方法生成trimap，然后使用Alpha matting获取到精细的mask。然后，作者使用这样的方法对几百张LDR图片生成了mask，统计个各类的亮度直方图，也即学习到了个各类的目标亮度。

在Tone mapping的部分，作者在HDR上获取到mask后，就简单的将目前的亮度替换为目标亮度，然后再用颜色恢复方法恢复出来LDR图像。

HDR10、HDR10+、HLG、Vivid、ACES资料解读

TODO https://en.wikipedia.org/wiki/Academy_Color_Encoding_System