原论文:https://people.csail.mit.edu/kaiming/sig13/index.html
摘要
拍摄全景照片的时候,因为人手在抖,所以可能拍出来的图片边界就不是一个矩形框。在本文中,作者提出了一种可以感知图片内容的弯曲(warp)算法,来将这种形状非矩形的图片转化为矩形图片。分为两步,第一步是没有mesh的,初步把一张图片弯曲成矩形。第二步就是在矩形中建立mesh,然后在其中优化图片,使得图片中的各种形状保持原样(例如直线保持直线的样子)。
简介
同上介绍的,关于拍摄全景照片,因为手抖,无法拉出一个矩形图片。
一个简单的解决办法是:剪裁。从这个图片中剪裁出一个矩形区域。缺点是会损失很多信息。还有一种方法就是在原来的图片边缘的外面进行图片合成,缺陷是,对于复杂的语义信息无法处理。
作者这里提出了一种只会引入“可接受”的、“不容易注意到”的扭曲,并且保护图片原本内容的方法。
前人工作
Image alignment and stitching
全景照片实际上是将多张照片缝合(stitching)在一起的。通常用某种图片上的特征,来将原照片全部投影到一个相同的坐标系下。
Projections
众所周知,3D场景投影到2D会不可避免地导致一些折叠的扭曲。例如透视投影,虽然可以保持直线的形状,但是其他物体的形状则会被拉伸。圆柱投影和球面投影可以保持物体的形状,但会弯曲直线。
也有研究者提出了一种在自适应流形(adaptive manifold)上进行投影和缝合的方法。不过它是适应相机的移动,而不是适应图片的内容。
之前也有大量的工作,考虑将这些折叠后的扭曲,通过某种方式,让它们出现在不容易注意到的位置。虽然视觉上可以接受,但是无法移除固有的扭曲。
Image retargeting and warping
Image retargeting是一种基于图片内容的缩放图片的方式。但是它们都假设输入的图片具有矩形形状,而且其中一部分必须还要定义一个grid mesh。
Image completion
即前面提到的,在图片的边缘增加内容,使其变成一个矩形图片。一般的方法是把图片里面的内容,复制到需要合成的地方。但是对于需要生成语义内容来说,表现不好。
算法
算法分为两部分,一部分是改进的Seam Carving,是一个Local Warp的步骤,其将图片初步弯曲成矩形。然后另一部分(global warp)在前一步的基础上,建立一个grid mesh,在mesh上进行优化,来保证原图的物体形状和直线形状不变。
Local Warp
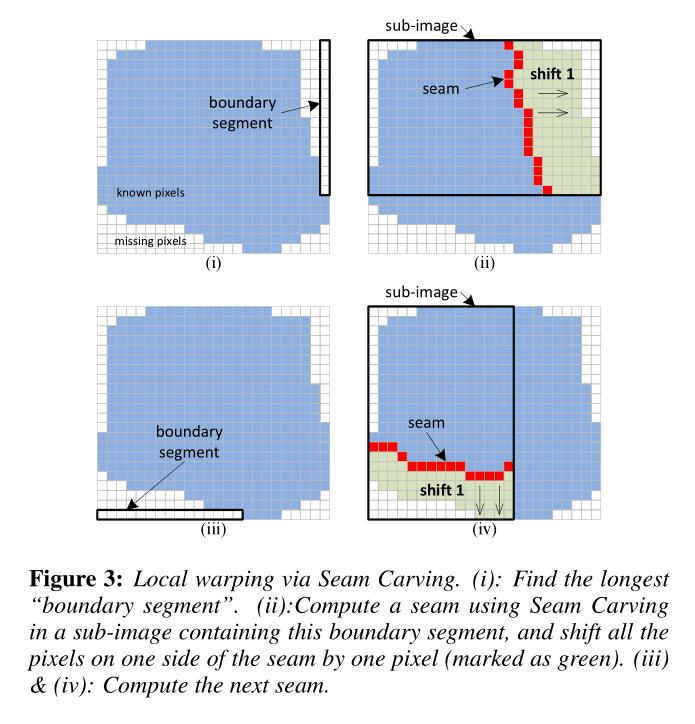
原版的Seam Carving算法是在图片中插入水平或者垂直的接缝(seam),来穿过整张图片,然后再从接缝中水平或者垂直地扩展一个像素。作者这里想到,接缝不穿过整张图片,这样就可以改变图片边缘的形状,从而变成矩形。
原版的算法可见https://faculty.runi.ac.il/arik/scweb/imret/index.html
如上图,其中蓝色的部分是有效的图片像素,白色的部分是需要我们填充的像素。
首先定义boundary segment是待填充像素中的,在图片顶部/底部/左侧/右侧的一行/一列像素。例如上图。我们找到目前最长的一个boundary segment,然后从它扩展得到一个sub-image。
这里左侧右侧的boundary segment,扩展出来的sub-image的高度保持,而宽度则等于整张图。同理,顶部和底部的boundary segment,扩展出来的sub-image的宽度保持,高度等于整张图。
然后我们在这个sub-image上利用seam carving的方法,去进行图像扩展。方法很简单,首先根据图片颜色梯度信息,计算每一个像素的能量。然后使用动态规划,求解最短路径。
以Figure 3(ii)为例,计算得到每个像素的能量。因为我们需要向右边填入像素,所以我们需要一个竖直方向的seam。于是我们用动态规划的方式,求底部像素到顶部像素的最短路(8邻居路径),然后所有底部像素中距离顶部像素最近的像素,及其到顶部的路径,成为我们的seam。
注意这里使用8邻居是源于原算法的研究,另外,我们需要给待填入的像素的能量赋值为\(10^8\)或者更大的数,来防止seam穿过这些像素。
填充像素的时候,我们把seam及其右边的像素都往右移动一位。原本seam的位置则求取左右两个像素的平均。
原版算法中提到,为了防止反复在相同的位置插入seam、导致如下的情况
之前的作者建议同时采集多根seam,然后依次填入像素。
但是这在我们这篇文章中是行不通的。我们的Local Warp要求我们每次填充完一根seam之后,都要重新计算最长的bound segment,我们不能反复对同一个sub-image填入像素。
我这里的实现采用了一个比较trick的方法,算出seam后,对原本的seam的位置的能量设置为\(10^5\)这样的数,比一般的大,比非法像素的小。之后让像素和能量都右移。现在原本的seam位置的能量和其右边一个像素的能量都为\(10^5\)了,这样就有更少的可能会在这里再次插入seam。
总而言之,重复以上过程,直到填充完所有像素。例如我实现的下例
其原图为
可以看到,虽然填充是填充了,但是歪歪扭扭。于是还需要下面的步骤。
Global Warp
Mesh Placement
首先,我们在Local Warp之后的图片的长宽上,将其分成\((40-1)*(10-9)\)个网格,其中\(40*10\)是网格的顶点数量。网格是正交的。
在Local Warp中,我们对像素进行了移动,我们需要记录下每个像素移动的偏移量。然后,我们使用网格顶点所在像素的偏移量,将各个网格顶点移动回去,就完成了mesh placement这一步。之后local warp的图像就可以抛弃了。移动后的结果例如:
Energy Function
这里设计能量的目的有三个,对于目前的网格与最终的网格结果之间:
- 保持网格的形状尽量不变,亦即Shape Preservation
- 保持网格内的线段的笔直,并且与其平行的其他线段,在处理后依然平行,亦即Line Preservation
- 网格上下左右贴合目标矩形图像框,亦即Boundary Constraints
Shape Preservation
最终输出的mesh的顶点(vertex)集记作\(V\),其中的每一个元素\(v_i=(x_i, y_i)\),可以用坐标表示出来。我们进行完Mesh Placement后得到的初始mesh记作\(\hat V\)
保型的能量定义为
\[E_S(V) = \dfrac{1}{N}\sum_q||(A_q(A_q^TA_q)^{-1}A_q^T-I)V_q||^2 \]
这里\(N\)是quad的个数。其中
\[A_q = \begin{bmatrix} \hat x_0 & -\hat y_0 & 1 & 0\\ \hat y_0 & \hat x_0 & 0 & 1\\ \vdots & \vdots & \vdots & \vdots\\ \hat x_3 & -\hat y_3 & 1 & 0\\ \hat y_3 & \hat x_3 & 0 & 1 \end{bmatrix} \]
\[V_q = \begin{bmatrix} x_0 \\ y_0 \\ \vdots \\ x_3 \\ y_3 \end{bmatrix} \]
这里也就是说第\(q\)个quad的四个顶点的坐标。其中\(A_q\)中的是初始mesh的坐标,\(V_q\)是目标mesh的坐标。
Line Preservation
我们目前计算过的东西是不包含“线段”这样的信息的。我们首先要做的事是,使用任何一种线段检测算法,来算出图片中的线段。
根据作者的说法,我们需要将这些线段切分开来,放到mesh的各个quad里。然后将所有线段的方向角(范围\([-\dfrac{\pi}{2},\dfrac{\pi}{2})\)),离散化为\(M=50\)个角度,每个离散化角度称为一个bin。为了保持直线性和平行性,设计的能量需要让每个bin里的线段拥有同样的角度。
给定一个线段,其方向向量\(e\)可以由线段的两个端点相减得到。如果我们将线段的两个端点用其所在的quad的\(V_q\)进行双线性插值表示,那么\(e\)就可以表示为\(V_q\)的线性函数。
同样的\(e\)是我们的目标,而\(\hat e\)则是最初的对应线段的方向向量。对于某一条线段,给定旋转操作的目标角度\(\theta_m\),它的能量为
\[||sR\hat e-e||^2 \]
其中
\[R = \begin{bmatrix} \cos\theta_m & -\sin\theta_m\\ \sin\theta_m & \cos\theta_m \end{bmatrix} \]
是旋转矩阵,而
\[s=(\hat e^T\hat e)^{-1}\hat e^TR^Te \]
是放缩因子。能量可以重新写为
\[||Ce||^2 \]
其中
\[C = R\hat e(\hat e^T\hat e)^{-1}\hat e^TR^T-I \]
因为\(\hat e\)和\(e\)都可以写作\(\hat V_q\)和\(V_q\)的线性函数,所以能量就可以写成二次函数。
总的能量为
\[E_L(V, \{\theta_m\}) = \dfrac{1}{N_L}\sum_j||C_j(\theta_{m(j)})e_{q(j)}||^2 \]
这里\(N_L\)为线段总数。对于第\(j\)条线段,\(\theta_{m(j)}\)代表其所属的bin中的目标旋转角度,\(q(j)\)代表其所属的quad。
Boundary Constraints
直白点说,就是把mesh的上下左右拉到图片框边缘上。
\[E_B(V) = \sum_{v_i\in L} x_i^2 + \sum_{v_i\in R} (x_i-w)^2 + \sum_{v_i\in T} y_i^2 + \sum_{v_i\in B} (y_i-h)^2 \]
\(L/R/T/B\)分别是左右上下边界的mesh顶点,\(w, h\)则是图片框的宽高。
最终能量
将前面的几个加和,添加权重
\[E(V, \{\theta_m\}) = E_S(V)+\lambda_LE_L(V, \{\theta_m\}) + \lambda_B E_B(V) \]
显然,我们需要图片至少能够贴合图片框,我们设置\(\lambda_B=10^8\)来确保这一点。然后,关于\(\lambda_L\)的选择,作者说选取\(>10\)比较好,原文采取了\(\lambda_L=100\)。
优化算法
作者指出,可以分别优化\(V\)和\(\{\theta_m\}\)。每各优化一次算迭代一次,总共迭代10次。
固定\(\{\theta_m\}\)优化\(V\)
此时能量函数是\(V\)的二次函数,可以求解线性方程来计算。总共就几百个顶点,所以总体上来说,这部分的开销很小。
这里的求解是通过最小二乘法来算的,具体见我自己的实现部分。
固定\(V\)优化\(\{\theta_m\}\)
因为另外两项和\(\theta\)无关,所以我们只用优化\(E_L\)这一部分。
作者指出,可以通过牛顿迭代等方法去优化。但是,几何意义上,\(E_L\)的目标是找到一个\(\theta_m\),使得所有在第\(m\)个bin中的线段\(e\)和其初始线段\(\hat e\)的夹角,都近似等于\(\theta_m\)。所以,我们可以简单的计算所有这个夹角,然后加和,求平均,作为新的\(\theta_m\)。
防止拉伸和后处理
如果我们的目标图相框的长宽比设置的不是很好,那么我们的结果图就会被拉伸。为了减少这种拉伸问题,我们在global warping之后更新目标框。
对于每个quad,我们计算它的\(x\)方向的伸缩因子为
\[s_x=(x_{max}-x_{min})/(\hat x_{max}-\hat x_{min}) \]
所有quad的平均伸缩因子就为\(\bar s_x\)。同理可以计算出\(\bar s_y\)。之后我们的目标框就设置为\((w/\bar s_x, h/\bar s_y)\)。
之后我们再在这个新的目标框上跑一次global warping
获得最终的mesh之后,我们就可以通过一些方法来获得最终的图像了。以图形学的思想为例,最终的mesh构成了我们要绘制的三角面。三角面空间坐标为最终mesh的坐标,uv坐标则是初始mesh的坐标。texture则是原图。
作者指出,这样的实现有一个小问题,因为mesh不会只包住有效像素,例如
这里的quad有一部分就包含了外部的无效像素。进行纹理采样时,作者简单地将无效像素替换为最近的有效像素。
实现细节
由于mesh是很“光滑”的,作者指出我们可以在缩小的图片上进行mesh的计算。首先将图片缩小到一个固定的大小,然后再在上面进行local/global warping。然后我们将mesh的尺度放大到原来的图片大小,再用这个mesh去进行纹理采样。
本文局限
如果图片缺失的部分太多,那么处理结果不好
本文的算法可能会导致边缘凹进去
作者指出,可以手动添加一个透明区域,当作已知像素。
将其当作已知像素来warp,之后在本文的算法处理完之后,再在这个透明区域中使用image completion等方法。
另外,本文无法处理未识别到的线段。这可以通过用户交互来缓解。
最后,本文无法应对线段数量过多的情况,这是warping方式的共同挑战。
我的实现
https://github.com/kegalas/Rectangling_Panoramic_Images
一些细节
首先是我之前也提到过的,为了防止反复在同一个地方插入seam,我们添加了额外的一个像素类别SEAM_PIXEL,让他的能量为\(10^5\)。比一般的像素大,比无效像素小。
在Global Warping主要要说明的部分则是关于如何优化能量。从\(E_S\)开始
\[E_S(V) = \dfrac{1}{N}\sum_q||(A_q(A_q^TA_q)^{-1}A_q^T-I)V_q||^2 \]
我们需要使其最小。众所周知,使向量的范数平方最小,只用使其每一维都最小即可。或者说,使向量尽可能成为零向量。
这里的\((A_q(A_q^TA_q)^{-1}A_q^T-I)\)是一个\(8\times 8\)矩阵(记作\(A\)好了),而\(V_q\)是一个8维向量。我们可以将所有的\(V_q\)收尾接在一起。如果我们的mesh是\(40\times 10\)的,那么新的拼接向量\(V_Q\)的维度就是\((40-1)\times(10-1)\times 8\)
\[V_Q = \begin{bmatrix} V_1 \\ V_2 \\ \vdots \\ V_{N-1} \\ V_{N} \end{bmatrix} \]
同理,我们也可以把\(A\)拼接。如下
\[A_Q = \begin{bmatrix} A_1 & & & \\ & A_2 & & \\ & & \ddots & \\ & & & A_N \end{bmatrix} \]
我们的目标是使得
\[E_S(V) = \dfrac{1}{N}A_QV_Q = \overrightarrow{0} \]
这里\(A_Q\)是用\(\hat V\)算的,而\(V_Q\)是我们最终mesh的坐标。也就是说我们需要解方程算出来\(V_Q\)。这其实就是最小二乘法。我们使用Eigen的QR分解对\(A_Q\)分解,然后再求解\(V_Q\)。这里建议使用稀疏矩阵。
另外,每一个mesh的顶点只能有一个实例,不能单纯地把所有quad的四个顶点放进去同一列。每个顶点只能出现在\(V_Q\)里一次。我们直接存储\(V_Q\)为\(40\times 10\times 2\)维向量。即每个顶点都只存一份(包含\(x,y\)坐标)。然后我们去修改\(A_Q\)的顺序就可以在向量乘法的时候一一对应。具体见我写的代码。调整后写为
\[E_S(V) = \dfrac{1}{N}AV = \overrightarrow{0} \]
接下来比较简单的是\(E_B\)
\[E_B(V) = \sum_{v_i\in L} x_i^2 + \sum_{v_i\in R} (x_i-w)^2 + \sum_{v_i\in T} y_i^2 + \sum_{v_i\in B} (y_i-h)^2 \]
对于mesh上的一个顶点\(v_i\),其有四种情况,在左侧、右侧、上部,下部。当然有四个顶点同时属于两种情况。也就是说,有一些顶点需要限制\(x\)坐标,有一些需要限制\(y\)坐标,有一些两个都需要限制,而有一些则两个都不需要限制。
设\(B_i\)如下
\[B_i = \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} \]
一个点如果需要限制\(x\)坐标,则\(a=1\),如果需要限制\(y\)坐标,则\(b=1\)。否则都等于\(0\)。
例如左上角的顶点\((x, y)\),我们的目标是
\[\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 0\\ 0 \end{bmatrix} \]
对于右下角的顶点,目标是
\[\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} w\\ h \end{bmatrix} \]
对于右侧的顶点,目标是
\[\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} w\\ 0 \end{bmatrix} \]
对于中间的无限制顶点,目标是
\[\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 0\\ 0 \end{bmatrix} \]
以此类推。
同样的,我们把\(v_i\)合并成一个\(40\times 10\times 2\)向量(同前)。将\(B_i\)也合并。
\[B = \begin{bmatrix} B_1 & & & \\ & B_2 & & \\ & & \ddots & \\ & & & B_N \end{bmatrix} \]
这里就不用重新调整\(B\)内容的顺序了。接下来合并目标\(v_{ti}\)
\[V_T = \begin{bmatrix} v_{t1} \\ v_{t2} \\ \vdots \\ v_{tn} \end{bmatrix} \]
最终的目标是
\[E_B(V) = BV = V_T \]
同样,Eigen解方程可得\(V_Q\)。
接下来是很复杂的\(E_L\)
设原始的一条线段为\(\hat L=[\hat x_{l0}, \hat y_{l0}, \hat x_{l1}, \hat y_{l1}]^T\)。根据我们前面的说法,一条线段会被mesh切割,然后放进各个quad中。我们用quad的四个顶点来进行双线性插值,来表示目标的\(L\)。方式如下,首先用双线性插值从\(\hat V_q\)计算出\(V_q\)
\[\begin{bmatrix} \hat x_0 & \hat y_0 & \hat x_0\hat y_0 & 1 & & & &\\ & & & & \hat x_0 & \hat y_0 & \hat x_0\hat y_0 & 1\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots\\ \hat x_3 & \hat y_3 & \hat x_3\hat y_3 & 1 & & & &\\ & & & & \hat x_3 & \hat y_3 & \hat x_3\hat y_3 & 1 \end{bmatrix}F_L = \begin{bmatrix} x_0\\ y_0\\ \vdots\\ x_3\\ y_3 \end{bmatrix} \]
我们把上式左边的\(8\times 8\)矩阵记作\(W\),上式就为\(WF_L=V_q\)
然后用\(\hat L\)表示\(L\),有
\[\begin{bmatrix} \hat x_{l0} & \hat y_{l0} & \hat x_{l0}\hat y_{l0} & 1 & & & &\\ & & & & \hat x_{l0} & \hat y_{l0} & \hat x_{l0}\hat y_{l0} & 1\\ \hat x_{l1} & \hat y_{l1} & \hat x_{l1}\hat y_{l1} & 1 & & & &\\ & & & & \hat x_{l1} & \hat y_{l1} & \hat x_{l1}\hat y_{l1} & 1 \end{bmatrix}F_L = \begin{bmatrix} x_{l0}\\ y_{l0}\\ x_{l1}\\ y_{l1} \end{bmatrix} \]
上式左侧\(4\times 8\)矩阵记作\(H\),上式就为\(HF_L=L\)
于是
\[L = HF_L = HW^{-1}V_q \]
\(H\)和\(W\)都为已知,所以\(L\)表示为\(V_q\)的线性函数。计算\(L\)的向量\(e\)使用两个端点相减,矩阵为
\[D = \begin{bmatrix} -1 & 0 & 1 & 0\\ 0 & -1 & 0 & 1 \end{bmatrix} \]
有
\[e = DL = \begin{bmatrix} -1 & 0 & 1 & 0\\ 0 & -1 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_{l0}\\ y_{l0}\\ x_{l1}\\ y_{l1} \end{bmatrix}= \begin{bmatrix} x_{l1}-x_{l0}\\ y_{l1}-y_{l0} \end{bmatrix} \]
\(E_L\)中的\(||Ce||^2\)中的\(e\)最终就表示为
\[\underset{(2, 1)}{e} = \underset{(2, 4)}{D}\underset{(4, 8)}{H}\underset{(8,8)}{W^{-1}}\underset{(8, 1)}{V_q} \]
而
\[C = R\hat e(\hat e^T\hat e)^{-1}\hat e^TR^T-I \]
其中\(\hat e\)已知,\(R\)只和\(\theta_m\)有关。可以直接算,与\(V_q\)无关。
同样的,我们把所有线段的\(e\)和其\(C\)拼接(具体见代码),有
\[E_L(V,\{\theta_m\}) = \dfrac{1}{N_L}Ce = \overrightarrow{0} \]
同样的,在优化\(V_q\)时,上式是\(V_q\)的线性函数,只需要用Eigen解方程即可。
最终,我们的目标是使得
\[E = E_S+\lambda_LE_L+\lambda_BE_B \]
最小,即
\[\begin{bmatrix} \dfrac{1}{N}A\\ \dfrac{\lambda_L}{N_L}CDHW^{-1}\\ \lambda_BB \end{bmatrix}V = \begin{bmatrix} \overrightarrow{0}\\ \overrightarrow{0}\\ V_T \end{bmatrix} \]
用Eigen求解出V即可。注意其中的\(CDHW^{-1}\)指的是每一个线段的矩阵拼接后的结果,具体拼接见代码。