摘要
分离出图像的前景和背景,对于图像编辑是很重要的。经典的image segmentation实现方式有两个,一是使用纹理(颜色)信息,例如魔棒工具。另一种是使用边缘信息,例如磁力套索(Intelligent Scissors)。本文介绍使用graph-cut来进行图像分割。本文提出了三方面的改进:优化迭代、优化用户交互、border matting的处理优化
简介
这里提到,所谓的“前景对象”的结果是一个alpha-matte,反应了前景和背景的比例。个人理解应该是,某个像素属于前景的可能性的大小和背景的可能性的比。本文想要实现保证高性能的前提下,不需要用户的过多交互,就能得到很好的效果。
高性能指:精准分割前背景,主观上可信的alpha值,可以处理模糊、混合像素(mixed pixels)、和透明度(透明的物体),前景图片不带有背景透过来的颜色。
用户交互的简易程度:作者举例了两个极端,一个是需要用户逐像素地点击前景,一个是只需要用户点击前景和背景的几个位置。
之前的交互式获取matte的工作
魔棒(Magic Band)
和PS里用到的魔棒差不多,就是选择容差,选择图片中点击区域附近在容差之类的像素。但是这个容差有时不容易选择。导致结果不好。
磁力套索(Intelligent Scissors)
和PS里的磁力套索差不多,用户需要在前景的边缘大概地移动鼠标,选取整个前景。缺点是如果背景太复杂,用户需要的操作会很多。
Bayes matting
对颜色概率分布进行建模,来实现一个full alpha mattes。用户要选取一个trimap。记作\(T=\{T_B,T_U,T_F\}\),其中\(T_B\)标记了背景,\(T_F\)标记了前景。之后alpha值是在剩下的那个区域\(T_U\)上计算的。有时效果还是不错的,但是只有当\(T_U\)区域不太大,并且前背景的颜色概率分布可以很好地分开时,效果才不错。另外,需要的用户操作也不少。
Knockout 2
是一个PS的插件,里面用的是用户定义的trimap,总体和Bayes matting差不多。
Graph Cut
优化了bayes matting,同样利用了trimaps和对颜色的概率分布建模,鲁棒性很好,它甚至可以区分出环境里的迷彩服。具体在第二节才会介绍。
Level sets
通过解偏微分方程来做。缺点是可能会陷入局部最优。
作者提出的系统:grabcut
理想状态中,一个matting工具应该能够在\(T_U\)上计算连续的alpha值,没有强制约束的话,alpha的值可能就只会是0、1两个值。如果有连续的alpha值,那么对于烟雾、头发、树(叶)等问题应该可以自动地、近似地解决。但是作者发现,对于前景背景颜色分布容易分开的图像效果还可以,遇到迷彩这样的东西就不行。
首先作者会在第二节和第三节介绍一个使用迭代图割(iterative graph cut)的方法来获取图像硬分割(hard segmentation)。然后在第四节border matting部分会用上通过硬分区之间的区域来计算alpha value。作者说,grabcut不处理完全透明的情况,除非是在border部分。作者建议使用matting brush来处理这种完全透明,只要没有迷彩,结果就可以很好。
作者认为,本文的首要创新在于处理图像的分割。他们为graph cut提供了两个优化:迭代估计、不完全标记。这两个东西可观的减少了用户交互的复杂度。只需要拖拽一个矩形框柱前景。另外,也开发出了一种新的计算alpha值的机制,来用于border matting的部分。
使用Graph Cut进行图像分割
grabcut是建立在graph cut的研究基础上的,所以有必要对此进行详细描述。
图像分割
graph cut是用于黑白图像分割的。给定一个初始的trimap,\(T\),图像是一个数组\(z=(z_1,\cdots,z_N)\),每个值都是灰度值,下标是一维的。图像的分割用一个“不透明度”的数组来表示,\(\underline{\alpha}=(\alpha_1,\cdots,\alpha_N)\)表示。每个像素都有一个这种数组。一般来说\(\alpha_n\)是\([0,1]\)上的实数,但对于硬分割来说,其取值为集合\(\{0,1\}\)。\(0\)代表背景,\(1\)代表前景。
参数\(\underline{\theta}\)描述图像前景和背景的grey-level概率分布,也包含了灰度值的直方图。即
\[\underline{\theta} = \{h(z;\alpha), \alpha=0,1\} \]
其中直方图是直接用\(T_B, T_F\)标记的像素得来的。这里直方图进行了归一化,\(\int_zh(z;\alpha)=1\)
图像分割的任务就是使用给定的\(z\)和\(\underline{\theta}\),来推断出未知部分的不透明度数组\(\underline{\alpha}\)
最小化能量法来进行分割
定义能量函数\(E\),其值最小化的时候,得到最好的分割结果。某种意义上,这个\(E\)应该和前景、背景的直方图都有关,并且也和不透明度有关。反应了物体的一种稳定趋势。作者从吉布斯自由能中获得了灵感,写出了一个类似的形式:
\[E(\underline{\alpha},\underline{\theta},z) = U(\underline{\alpha},\underline{\theta},z)+V(\underline{\alpha},z) \]
其中,数据项\(U\)在给定直方图模型\(\underline{\theta}\)的情况下,评估不透明度分布\(\underline{\alpha}\)对图像\(z\)的拟合。定义为
\[U(\underline{\alpha},\underline{\theta},z) = \sum_n-\log h(z_n;\alpha_n) \]
其中,平滑项为
\[V(\underline{\alpha},z) = \gamma\sum_{(m,n)\in C}dis(m,n)^{-1}[\alpha_n\neq\alpha_m]\exp-\beta(z_m-z_n)^2 \]
里面的\([...]\)是一个艾弗森括号。\(C\)是一个集合,里面的元素是邻居像素点对。\(dis(\cdot)\)是邻居像素点对的欧拉距离。这种能量(指平滑项)让灰度相似的区域更加具有一致性。实践中,像素的邻居有8个。
当常数\(\beta=0\)时,平滑项就简化为著名的Ising prior(但我不知道是什么)。此时平滑项就对全图进行平滑,其程度由\(\gamma\)决定。在Graph Cut的论文中指出,设置\(\beta>0\)更好,这可以放松对于高对比度区域的平滑,同时这里的\(\beta\)可以选为
\[\beta = \bigg(2\bigg<(z_m-z_n)^2\bigg>\bigg)^{-1} \]
这里\(<\cdot>\)代表图像上样本的期望。选这个\(\beta\)能够保证,平滑项可以适当的从高对比度和低对比度场景中切换。
常数\(\gamma\)取\(50\),这是后面的文章通过实验得到的经验值。
在定义完能量模型后,图像分割就可以被估计为
\[\underline{\hat{\alpha}} = \arg\min_{\underline{\alpha}} E(\underline{\alpha}, \underline{\theta}) \]
这里的最小化使用最小割算法。这也是硬分割的基础。
下一部分会介绍作者三方面的改进。首先是把黑白图像的模型,用高斯混合模型替换,从而可以用到彩色图像上。第二,执行一次最小割的算法被替换为一个迭代过程。第三,简化用户操作,只需要使用一个矩形或者一个套索来标注\(T_B\)
如何用网络流为该问题建模?
这里是GrabCut在介绍GraphCut时没有介绍到的,所以只读这篇论文我们根本不知道如何建图。
GraphCut论文:https://ieeexplore.ieee.org/document/937505
GraphCut的作者其实给出了更为泛用的理论,而不仅仅是黑白图像的处理。在这篇论文里,能量定义为
\[E(A) = \lambda R(A)+B(A) \]
这里的\(A\)即为之前提到的\(\alpha\),是硬分割。\(R(A)\)是区域项,\(B(A)\)是边缘项。
\[R(A) = \sum_{p\in P} R_p(A_p) \]
\[B(A) = \sum_{\{p,q\}\in N} B_{\{p,q\}}[A_p\neq A_q] \]
这里的\(P\)是所有像素的集和。\(N\)是相邻像素对的集合,其中\(\{p,q\}\)是无序的。
一般的\(\lambda\geq 0\)。\(R(A)\)代表着,给某个像素预测为前景和背景的惩罚。而\(B_{\{p, q\}}\geq 0\)则是边缘差异的惩罚,两个相邻像素\(p,q\),如果它们的颜色非常相近,那么\(B_{\{p,q\}}\)应该非常大;而颜色差异很大时,边缘项会非常接近\(0\)。
这里只是给出了泛用的理论,具体怎么去定义这些东西,看大家的具体问题。比如GrabCut就定义了自己的两个惩罚项,本文后面也针对黑白图像定义了惩罚项。
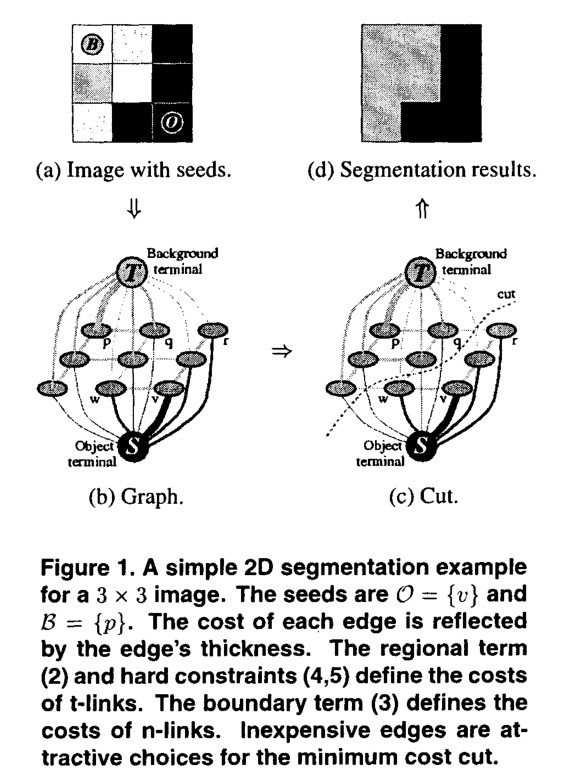
建图是像上面一样的,其中邻居像素之间有\(N-Links\),虽然它只画出来4个邻居,但是一般我们也会连上对角的邻居,作为8邻居。每个像素都和源点、汇点有一条边,称作\(T-Links\)。
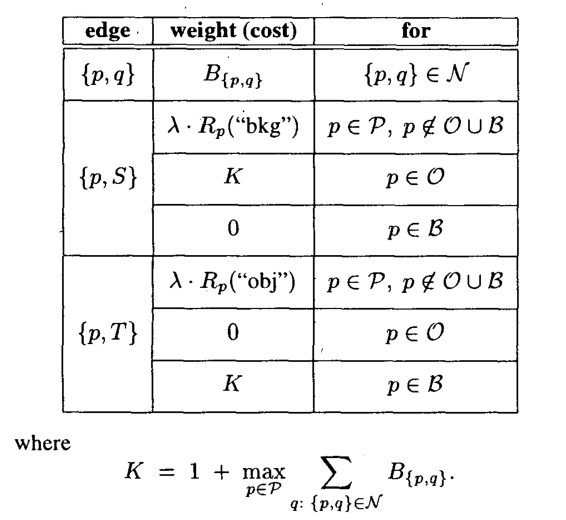
建图如上,邻居间的\(N-Links\)倒是非常简单,直接就是\(B_{\{p, q\}}\)。对于\(T-Links\)则更难一些。
首先要说明,求出最小割后,在源点一侧的节点是前景,在汇点一侧的节点是背景。所以,要给\(\{p, S\}\)这样的边一个误判为背景的惩罚项。图中\(O\)即为\(T_F\),\(B\)即为\(T_B\)。如果已经由用户定义了前景和背景,那么其权值就是固定的\(K\)或\(0\)。
在跑完最小割后,原本属于\(T_U\)的节点就可以根据自己属于源点部分还是汇点部分,分类到前景背景中了。
下面我们来讨论为什么最小割可以最小化能量。割即对于图\(G=(V,E)\),将点划分为\(S\)和\(T=V-S\)两个集合,其中源点\(s\in S\),汇点\(t\in T\)。割的容量即为所有\(S\)到\(T\)的边的容量之和,记为\(c(S,T)\)。最小割即为,使得\(c(S,T)\)最小的割。
首先是关于\(N-Links\),显然,两个像素颜色差异越大,这里越有可能是前背景的边界,而差异大的时候边权接近\(0\),所以这样的\(N-Links\)必然会出现在最小割中。
然后是关于\(T-Links\),一个像素如果被误判的惩罚项很大,比如前景误判为背景,那么它更有可能是前景。我们只能牺牲局部,保全大局,将误判惩罚最小的项让出去,来实现局部最优。所以这样的\(T-Links\)也会出现在最小割中。这里的\(K\)这是一样的,例如\(\{p,S\}\)中的\(K\),如果一个像素已经定义为属于前景了,那么其被误判为背景的惩罚应该很大,如果一个像素已经是背景了,那么其被“误判”为背景的惩罚应该为\(0\)。
GrabCut图像分割算法
这一部分也是硬分割的。
对彩色图像数据建模
现在图像是RGB三通道的了,再像以前一样去构建灰度直方图是不切实际的(从256变成了\(256^3=\) 17M)。
作者这里参考前人的工作,对前景和背景各使用一个GMM,其\(K\)值都等于\(5\)。简便起见,在优化框架框架中,添加了一个向量\(k=\{k_1,\cdots,k_n,\cdots,k_N\}\),其中\(k_n\in\{1,\cdots,K\}\)。为每个像素分配一个不同的GMM分量,根据\(\alpha_n=0\)还是\(1\)来确定分配前景还是背景GMM分量。
此时,吉布斯能公式变为
\[E(\underline{\alpha},k,\underline{\theta},z) = U(\underline{\alpha},k,\underline{\theta},z)+V(\underline{\alpha},z) \]
现在数据项\(U\)变为
\[U(\underline{\alpha},k,\underline{\theta},z) = \sum_nD(\alpha_n,k_n,\underline{\theta},z_n) \]
\[D(\alpha_n,k_n,\underline{\theta},z_n) = -\log p(z_n|\alpha_n,k_n,\underline{\theta})-\log\pi(\alpha_a,k_n) \]
其中\(p\)是正态分布,\(\pi\)是高斯混合模型中的那个混合系数。展开有
\[D(\alpha_n,k_n,\underline{\theta},z_n) = -\log\pi(\alpha_n,k_n)+\dfrac{1}{2}\log\det\Sigma(\alpha_n, k_n)+\dfrac{1}{2}[z_n-\mu(\alpha_n, k_n)]^T\Sigma(\alpha_n, k_n)^{-1}[z_n-\mu(\alpha_n, k_n)] \]
此时模型的参数为
\[\underline{\theta} = \{\pi(\alpha, k), \mu(\alpha, k), \Sigma(\alpha, k), \alpha=0,1,k=1,\cdots,K\} \]
平滑项几乎没变
\[V(\underline{\alpha},z) = \gamma\sum_{(m,n)\in C}[\alpha_n\neq\alpha_m]\exp-\beta||z_m-z_n||^2 \]
这里的距离变成了颜色空间中的欧拉距离。
能量最小化迭代法来进行图像分割
GrabCut使用了迭代的算法来替代Graph Cut的一次性算法。好处在于我们可以通过迭代来不断地精炼不透明度\(\underline{\alpha}\)。然后对于初始的trimap中的\(T_U\)部分的新标记,被用于精炼GMM的参数\(\underline{\theta}\)。算法见下图
首先是初始化部分
- 用户用矩形框框选前景,那么方框外的东西就是\(T_B\)了,而方框内的东西都是\(T_U\),即还未确定是否是\(T_F\)
- 对\(T_B\)内的每个像素初始化\(\alpha_n=0\),对\(T_U\)内的每个像素初始化\(\alpha_n=1\)
- 然后我们就得到了属于背景的像素和属于前景的像素,这时候就可以初始化GMM的参数了。首先分别对前景和背景的像素,分别用k-means聚类为\(K\)类,即得到GMM中的\(K\)个高斯模型的元素。然后对每个高斯模型的元素计算均值、协方差,然后混合系数也可以通过计算属于第\(k\)个高斯模型的元素占全体元素的比例来得到。
迭代过程:
- 对每个像素分配GMM中的高斯分量。\(k_n\)即为使得\(D_n\)最小的那个\(k_n\),公式见上图
- 对于给定的图像\(z\),学习优化GMM的参数。
- 使用最小割来进行图像分割。
- 重复步骤1-3直到收敛。作者指出,由于能量是一直递减的,所以一定会收敛。至少会收敛到局部最优。
- 应用第四节提到的border matting
用户编辑过程:
- 编辑:人为地固定一些像素为背景或前景,来更新trimap,然后执行一次第3步。
- 重操作:(可选)重复整个迭代过程。
用户人工编辑
GrabCut是根据颜色分布和边缘来进行图像分割的,但是也有一些“不合常理”的图片。此时还是需要进行人工的编辑。
Incomplete trimaps
这里指的应该就是,框选前景,反过来标记背景的操作。整个迭代算法也是不对\(T_B\)进行retract,但是\(T_U\)中的像素就可以被改变为背景或前景。
Further user editing
即前面描述的用户编辑过程。如果分割的图像错误地把一些东西分到了背景,则我们可以用前景刷把他们标记回来。反之亦然。
透明度处理
一个matting的工具应该可以处理连续的\(\alpha\)值。作者提出了一种机制,来使得之前的硬分隔增强为软分割,从而更好地处理物体边缘。
Border Matting
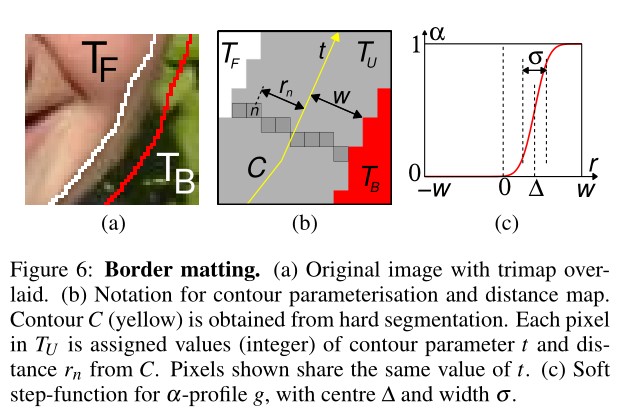
这个Border Matting一般是在一个闭合的曲线\(C\)上进行的,这条曲线一般是根据之前的硬分割的两部分的边缘组成的多边形。此时我们定义一个新的trimap\(\{T_B, T_U, T_F\}\),这里的\(T_U\)定义为\(C\)往外扩展\(w\)个像素(作者使用\(w=6\))。之后会使用动态规划来在\(T_U\)上来进行\(\alpha\)值的预测。
将曲线\(C\)参数化为\(t=1,\cdots ,T\),其中\(T\)是周期,因为\(C\)是闭合曲线。定义\(t(n)\)为\(T_U\)上的第\(n\)个像素组,这个组如下图(b)中的黑框灰色像素。
\(\alpha_n\)定义为\(\alpha_n=g(r_n;\Delta_{t(n)},\sigma_{t(n)})\),其中\(g\)是一个“软”阶跃函数,见上图(c)。\(r_n\)是像素\(n\)到曲线\(c\)的有正负的距离,见上图(b)。\(\Delta,\sigma\)的意义见上图(c),这里假设所有像素,如果它们的\(t\)相同,那么就拥有同样的\(\Delta, \sigma\)。
\(\Delta, \sigma\)是使用动态规划来求解的。最小化如下的能量
\[E=\sum_{n\in T_U} \widetilde{D}_n(\alpha_n)+\sum^T_{t=1}\widetilde{V}(\Delta_t,\sigma_t,\Delta_{t+1},\sigma_{t+1}) \]
其中\(\widetilde{V}\)是光滑正则项
\[\widetilde{V}(\Delta,\sigma,\Delta',\sigma')=\lambda_1(\Delta-\Delta')^2+\lambda_2(\sigma-\sigma')^2 \]
它的作用是,使\(t\)在增加时,\(\alpha\)的变化更为平滑。作者使用\(\lambda_1=50, \lambda_2=10^3\)。在DP过程中,\(\Delta_t\)的值有30个levels,而\(\sigma_t\)有10个levels。作者说它们的DP是线性时间的(我没看具体实现),需要两次遍历整个曲线\(C\)。
数据项\(\widetilde{D}\)定义为
\[\widetilde{D}_n(\alpha_n)=-\log N(z_n;\mu_{t(n)}(\alpha_n), \Sigma_{t(n)}(\alpha_n)) \]
\(N\)即为多元高斯正态分布,其中均值和方差为
\[\mu_t(\alpha) = (1-\alpha)\mu_t(0)+\alpha\mu_t(1) \]
\[\Sigma_t(\alpha) = (1-\alpha)^2\Sigma_t(0)+\alpha^2\Sigma_t(1) \]
这里的\(\mu_t(x),\Sigma_t(x),x=0,1\)是从前景和背景中的像素样本估算来的。前景\(F_t=S_t\cap T_F\),背景\(B_t=S_t\cap T_B\),这里\(S_t\)是一个矩形区域,即曲线\(C\)上的某个点\(t\)扩张\(L\)个像素得到的\(L\times L\)区域,作者取\(L=41\)
前景估计
作者指出,之前的Bayes matting方法,会有背景的颜色渗出到前景中的问题。作者这里通过从\(T_F\)中借用像素,来避免这个问题。
Bayes matting从\(n\in T_U\)中预测得到一个前景色\(\hat f_{n}\)。根据之前定义的\(F_{t(n)}\),可知\(\hat f_n\)会和借用的\(f_n\)很相似。
其他思考内容
GMM换成彩色直方图会怎么样?
以我自己的实验经验来说,\(256^3\)的内存空间还是放得下的,但显然不是内存的原因,才导致作者不去使用颜色直方图。我实际测试过,其效果比较差。如果你定义某个像素属于前景和背景的概率,仅仅考虑该像素颜色在直方图中的概率的话,只会有很少的像素被去除。如果你定义该概率为该像素RGB都\(\pm 5\)的这个范围内的概率和,则计算量就爆炸了,而且效果也不好。
其主要的问题在于,颜色在色彩空间中分布过于分散,计算概率的效果不好。
彩色直方图的其他优化方法
https://mmcheng.net/zh/salobj/
这篇文章中,作者指出,一张照片的绝大多数颜色(95%)都是相近的,可以将颜色空间简化到\(12^3\),即\(L*a*b*\)每个通道都简化为\(12\)个值。然后通过进一步的统计,选择其中出现次数最多的\(85\)个颜色,来覆盖\(95\%\)的图片色彩。
当然,为了应对剩下的那\(5\%\),使用与其最近的颜色替代。作者也提出了一个色彩空间平滑的操作,来解决噪声问题。有机会再来精读这篇文章。