网络设备管理
题目描述
叮叮叮!网络设备管理员欢欢在行动
欢欢就职于一家庞大的数据管理分析公司
公司有一个存储数据的庞大网络,把每个数据存储器看做一个节点,这个存储网络可以看做是一个树型结构,每天有庞大的数据流在节点之间穿梭
随着公司的发展,这个网络越来越庞大,数据的传输速度也越来越慢,通过研究,欢欢发现,每个节点的传输速度,只与与这个节点连接的节点数量有关,比如仅和一个节点连接的节点传输数据会很快,而和 100 个节点连接的节点传输数据会很慢
欢欢准备提交一份研究报告,报告将会指出,若对于网络中的所有节点,与该节点相连的节点数量不超过 d,那么网络的整体传输速度将会大幅提高。
欢欢准备通过添加新的网络设备来降低与某节点相连的节点的数量
简而言之,对于网络设备a,我们可以添加新的设备b,使得原来与a相连的若干节点断开与a的连接并与b连接,并且使a,b连接,显然,添加新的网络设备后,这个网络仍旧是一个树形结构这样通过添加若干新的网络设备,我们可以把所有网络设备的相连网络设备数量降低到不超过d台 (包括与新添加的网络设备相接的网络设备数量不超过 d)
欢欢发现,有很多种解决方案
聪明的你知道欢欢最少添加多少台网络设备吗?
注意: 欢欢添加新的设备后,网络的结构仍保持为树形结构
输入
单组输入 第一行两个正整数 \(n\), \(d$ \)(1\le n\le 10^5,3\le d\le n)\( 接下来\)n-1\(行,每行两个正整数$a\),\(b$ \)(1\le a, b\le n)\(,说明设备$a\)与设备\(b\)相连接,数据保证设备网络为树形结构。
输出
一个正整数,最小添加的网络设备数量,注意欢欢可以添加0台设备。
样例
| 样例输入 | 样例输出 |
|---|---|
| 10 3 2 1 3 1 4 1 5 2 6 1 7 6 8 5 9 7 10 6 |
1 |
AC代码
#include <iostream>
#define MAXN 100005
using namespace std;
int arr[MAXN];
int main(){
int n,d;
cin>>n>>d;
for(int i=1;i<n;i++){
int a,b;
scanf("%d%d",&a,&b);
arr[a]+=1;
arr[b]+=1;
}
int ans=0;
for(int i=1;i<=n;i++){
if(arr[i]>d){
int tmp = (d-1)*2;
if(arr[i]-tmp<=0){
ans+=1;
}
else if((arr[i]-tmp)%(d-2)==0)
ans += 1 + (arr[i]-tmp)/(d-2);
else
ans += 1 + (arr[i]-tmp)/(d-2)+1;
}
}
cout<<ans;
return 0;
}
正确性证明
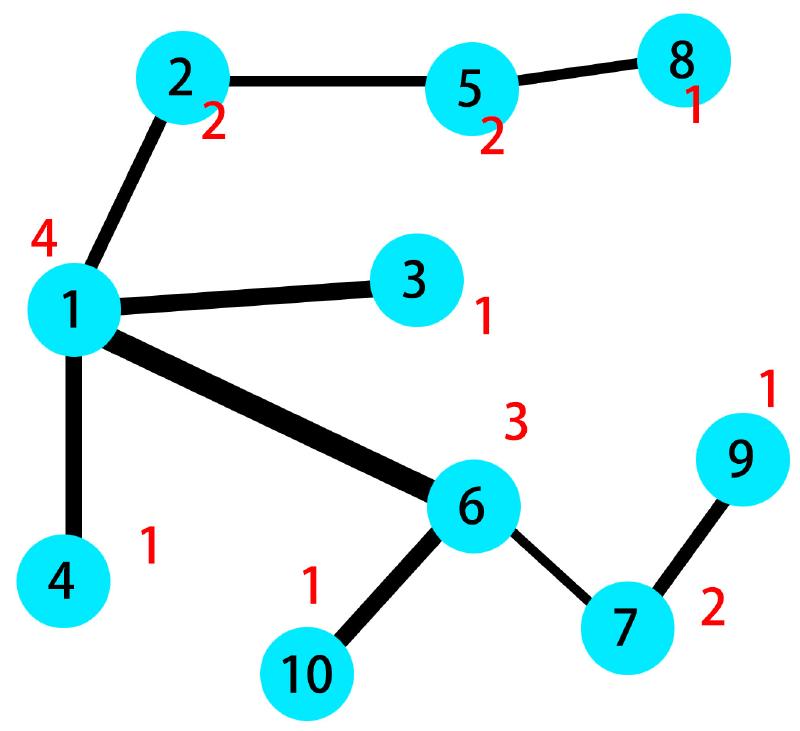
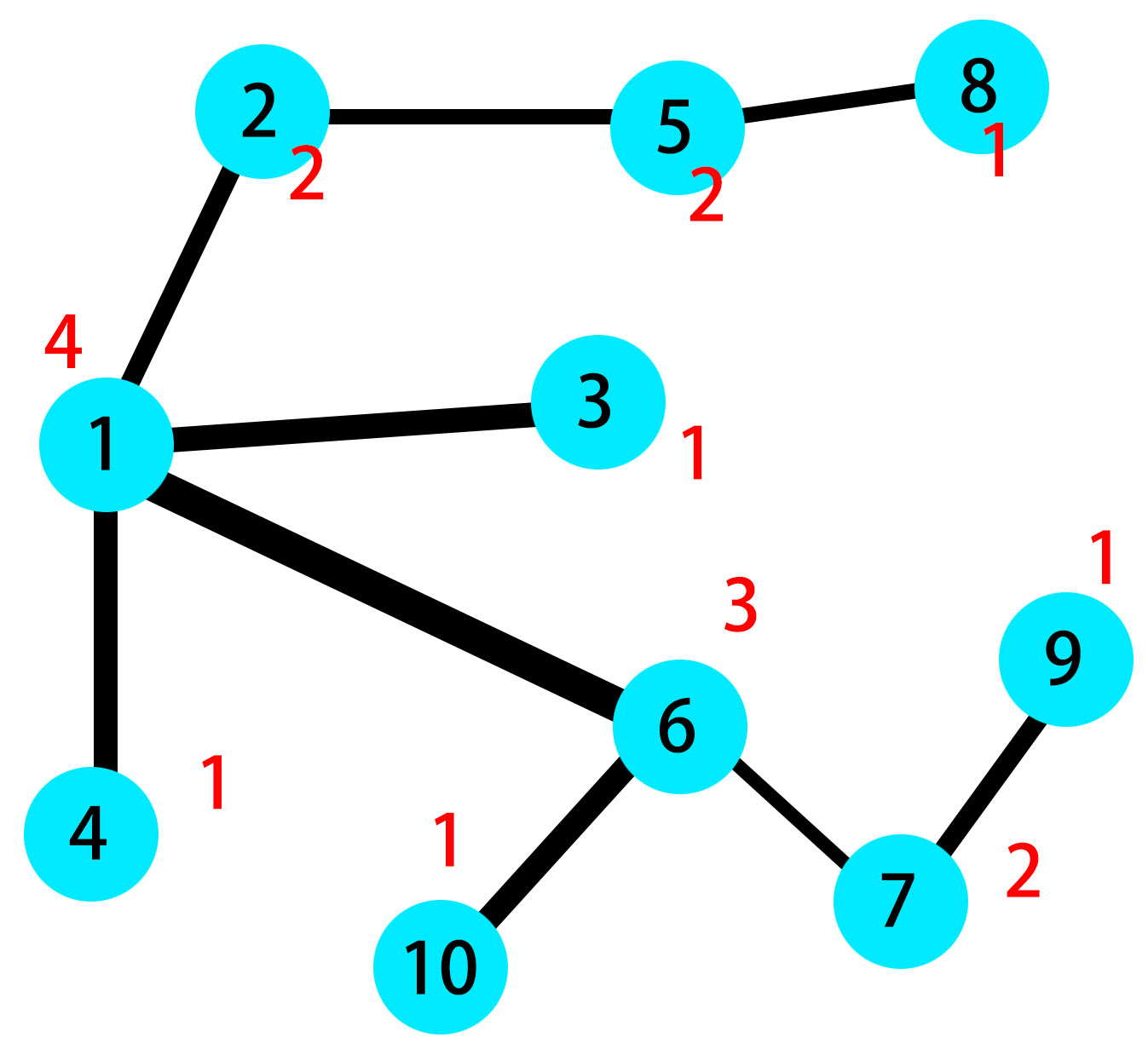
先给出样例的示意图
其中红色数字表示与这个节点直接相连的节点的个数。显然只有1号节点连了大于3个节点,我们可以新增一个节点A,将2、3号与A相连,4、6号不变,然后将1与A相连,现在1与A连了三个节点,符合要求。不过这不是唯一的连法。
这种有最大连接节点的结构,很容易让人回想起烷烃。显然的,饱和烷烃的碳链无论怎么排布,所连的氢原子的数目不会改变。每个碳原子也都会连四个原子。
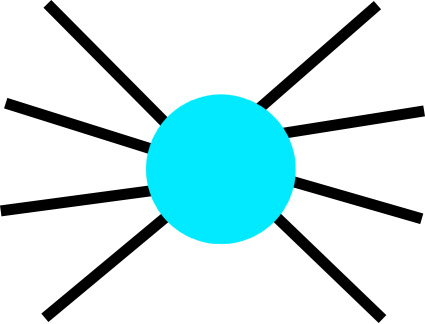
类比到这道题,我们要做的,就是将形如下图的点(假设上限为连3个)
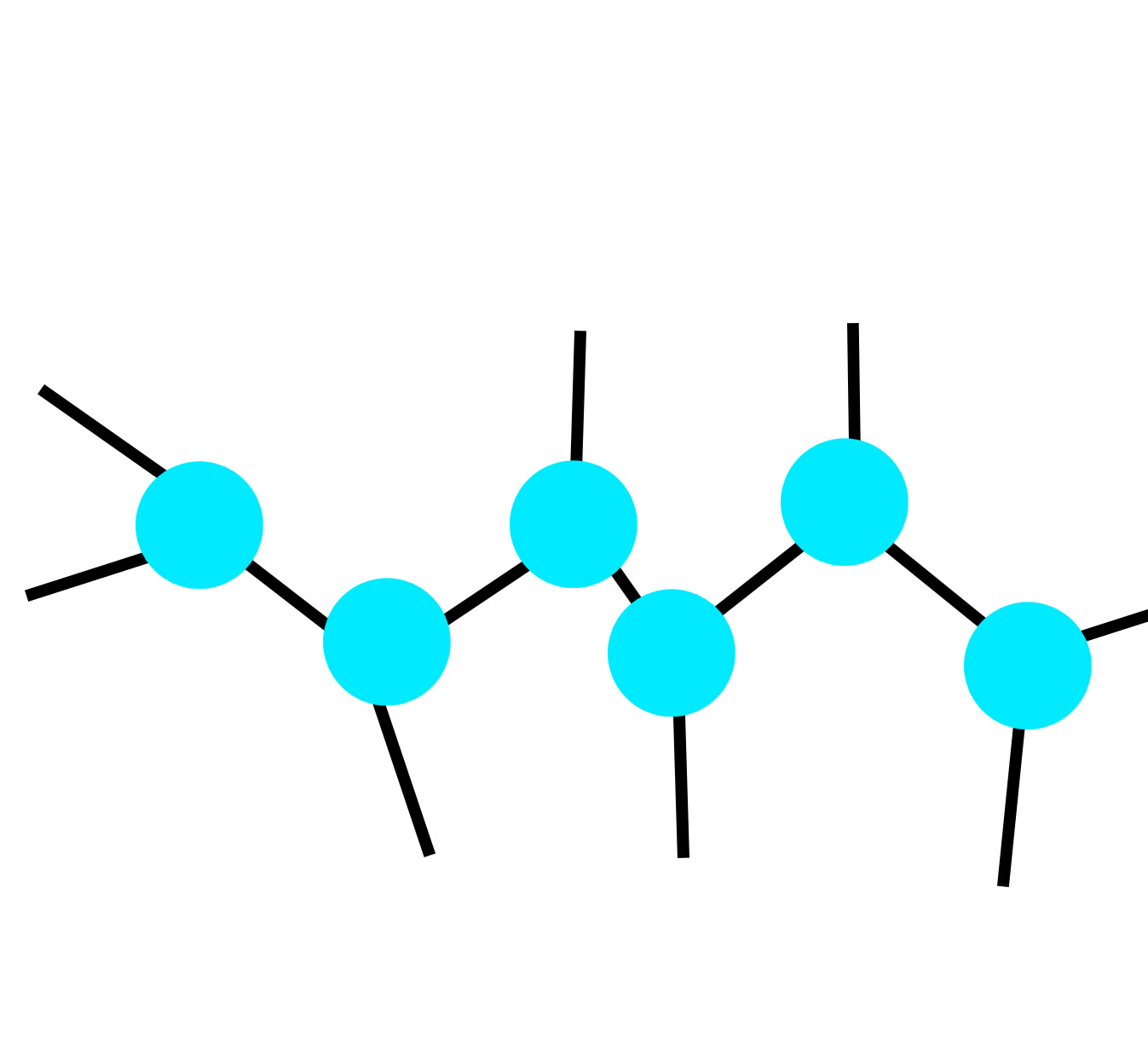
变为如下的一些点,当然这里的点怎么排布都不影响,只要他最大的利用了链接上限,就是答案。
解释一下核心代码
for(int i=1;i<=n;i++){
if(arr[i]>d){//枚举超过链接上限的节点
int tmp = (d-1)*2; //点链两端,能“向外”链接d-1个点,必须要向“内部”链接一个点,才能构成点链,这个arr[i]-tmp得到的是还需要“向外”链接的数量。
if(arr[i]-tmp<=0){//特判一下,如果只用新增一个节点,并且有一个节点没有占满上限
ans+=1;
}
else if((arr[i]-tmp)%(d-2)==0)//内部每个节点都只能“向外”链接d-2个节点,如果能全部占满每个内部节点的上限,ans如下
ans += 1 + (arr[i]-tmp)/(d-2);
else//不能占满则ans如下
ans += 1 + (arr[i]-tmp)/(d-2)+1;
}