前言
这篇文章是接在相机PSF标定之后的,我们也说过,PSF表征着光学系统的所有像差(除了畸变),也就描述了相机拍摄出来的照片是如何变得模糊的。我们获得PSF的目的实际上就是去校正这个相差,将图片中模糊的地方变得清晰。理论上来说,任何一种PSF标定方法得出的PSF都可以无缝接在这里面的所有像差矫正方法之前。
Extreme-Quality Computational Imaging via Degradation Framework
之前的部分见上一篇博客,在预估完PSF后,就介绍了本文的校正模型。
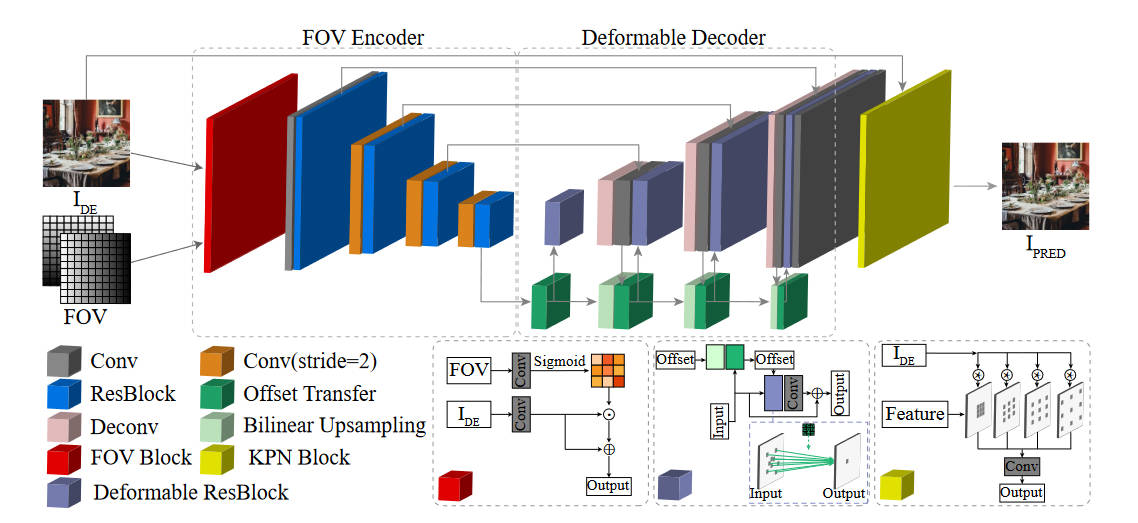
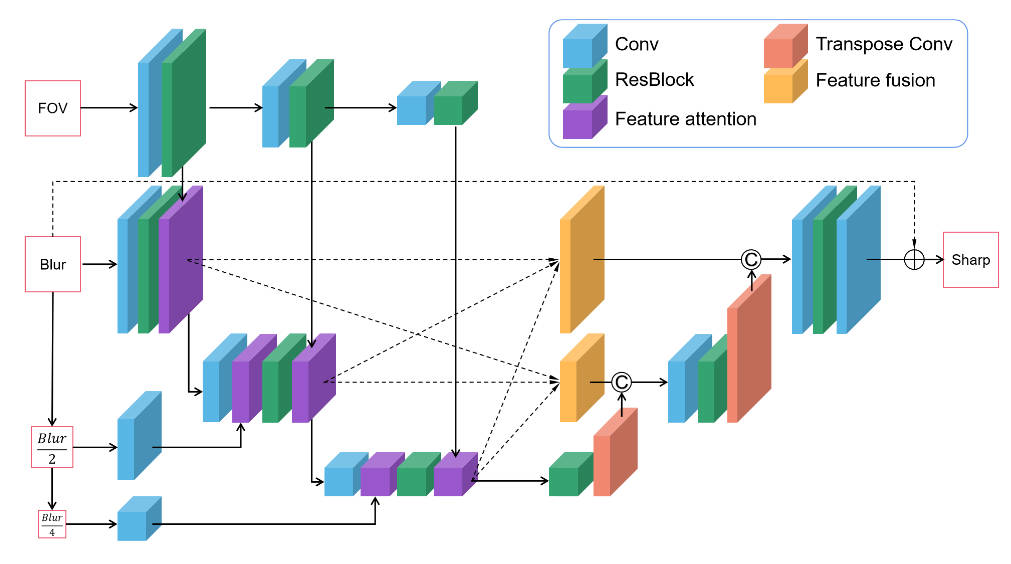
这是一个端到端的网络,输入一个退化的sRGB图像\(I_{DE}\),输出重建后的图像\(I_{PRED}\),大体上可以分为三个模块。
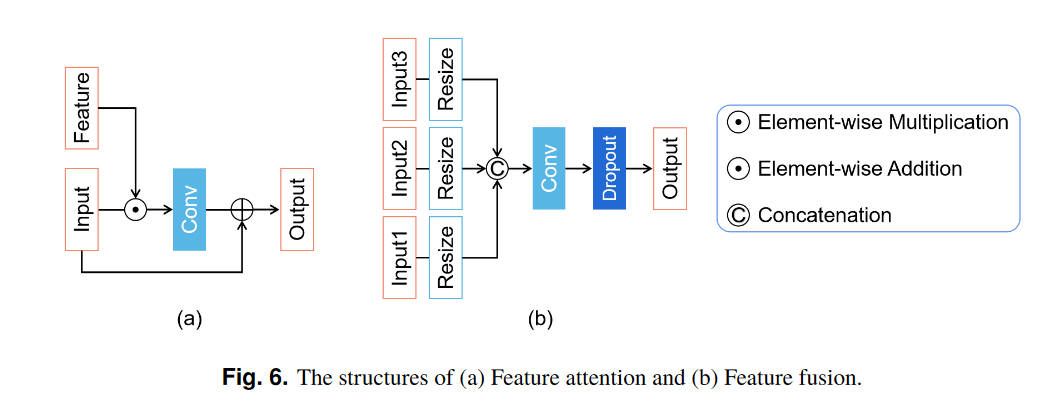
首先是FOV编码器。因为空间信息和退化有强相关性,本文提出了FOV模块来利用空间特征。这个网络的细节在上图的下方,可以看到它被用于计算一个mask,然后影响到\(I_{DE}\)的输出。
第二部分是一个可变形解码器。由于PSF的不规则形状和大小,传统的卷积层不是很适合来处理退化,因为传统卷积层只会获取到固定位置的特征。
最后一部分是KPN模块。按照前人的研究结果,预测卷积核来间接预测结果要比直接预测结果要更稳定一些,但是这会增加模型的开销,尤其是卷积核很大的时候。于是本文提出了一种扩大卷积的方式,来让卷积核影响更广的范围。可以看图像来理解。
我们预估的PSF到底用在哪里了呢?实际上在预估完PSF后,我们将ground truth与其进行卷积,合成退化图像。后面的恢复网络在这个配对数据上进行训练。
Large depth-of-field ultra-compact microscope by progressive optimization and deep learning
https://www.nature.com/articles/s41467-023-39860-0
本文主要是针对手机相机进行优化,让它能够较好的实现显微任务。作者指出过往的端到端方法计算开销太大,所以本文提出了一种渐进式的优化方法。
首先第一个需要优化的是镜头设计。首先考虑传统的镜头设计方法,例如光线追踪等等,来手动设计一系列镜头,后续的优化算法在每个镜头上都进行一次,选出最好的那一个。使用这种方法减小了参数量,从而减小开销。
关于镜头是如何设计的笔者不懂,也不是PSF估计的重点,就跳过。但是我们需要记得一些概念。在设计镜头的时候要考虑一个两难问题:景深和横向分辨率的关系,横向分辨率越大,景深越小。而对于一个显微镜来说景深是比较重要的。传统的增加景深的做法是减小数字孔径(NA),也就通常意味着减小物理孔径(光圈)或者增大焦距。但是减小光圈会导致进光量减小,从而减小信噪比;而增长焦距则会增大体积,对手机这种设备来说是不行的。
为了解决这个问题,本文开发了一种叫diffractive optical element (DOE)的物理元件,放在光圈之前。这个DOE在这里是一个三次曲面,表示为\(\alpha(x^3,y^3)\)。这里的\(\alpha\)是唯一一个参数,用于控制在不同的defocus(离焦)下PSF的扩散,从而控制景深大小。
针对这个\(\alpha\),本文均匀选择了\([0.005,0.075]\)上的15个值,每一个都做成一套系统(顺带一提材料便宜、工艺简单、成本很低),然后在神经网络上训练,选出最好的。最后选出来的是\(\alpha=0.03\),使得景深增加了10倍。
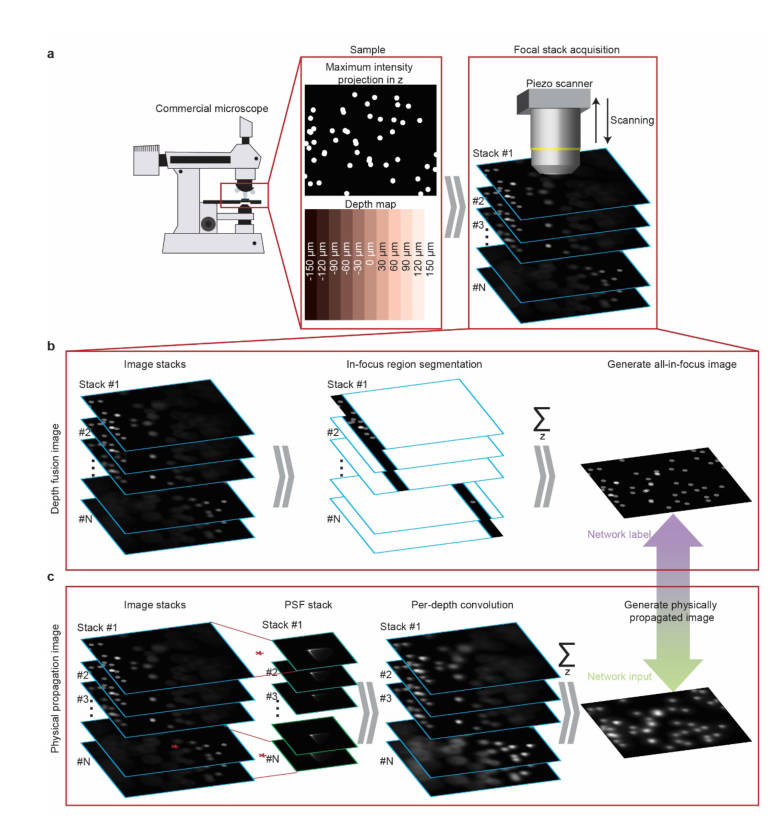
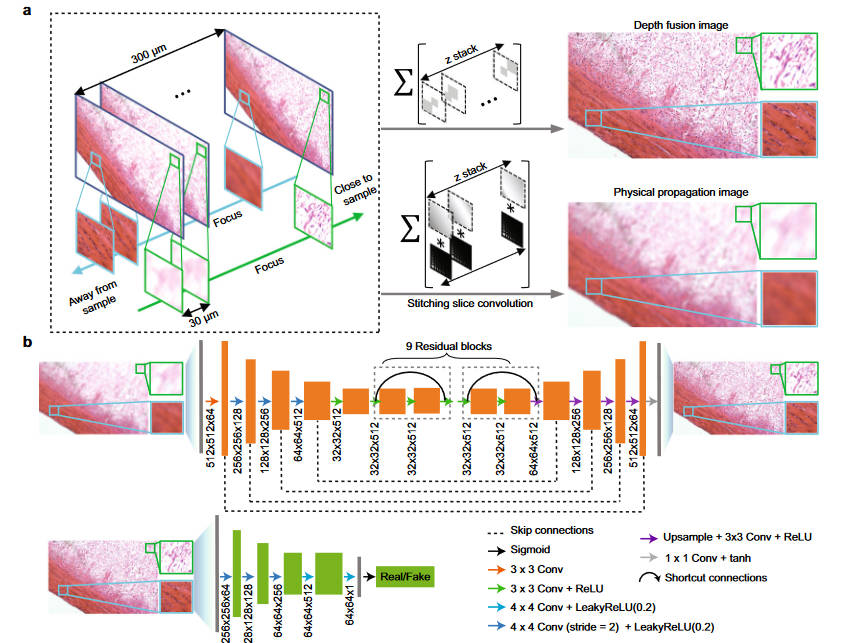
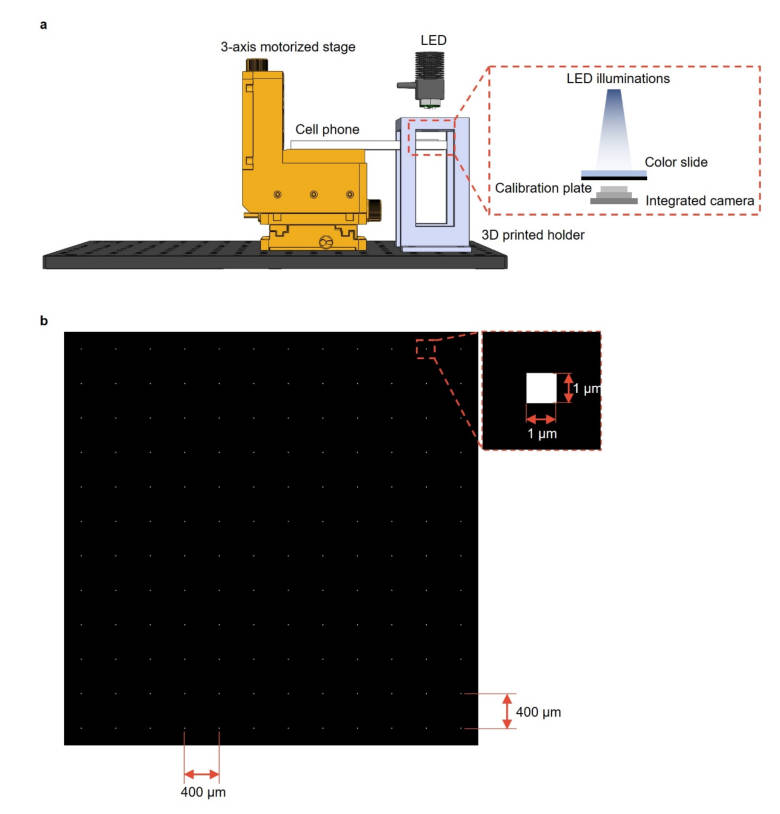
网络架构基于pix2pix,可以很好的适应细节丰富的图像复原任务。本文获取训练数据的方式是,使用商用的显微镜,上下调节物镜高度,获得一系列图像
其中使用算法将每张图片中最清晰的部分提取出来,合并成一个all-in-focus图像,作为Ground-Truth。然后对每一张图片,使用本文设计的镜头在对应高度下的PSF进行卷积,最后再合并起来,得到近似的本文镜头拍摄的退化图象。二者作为配对数据送入pix2pix中进行训练。
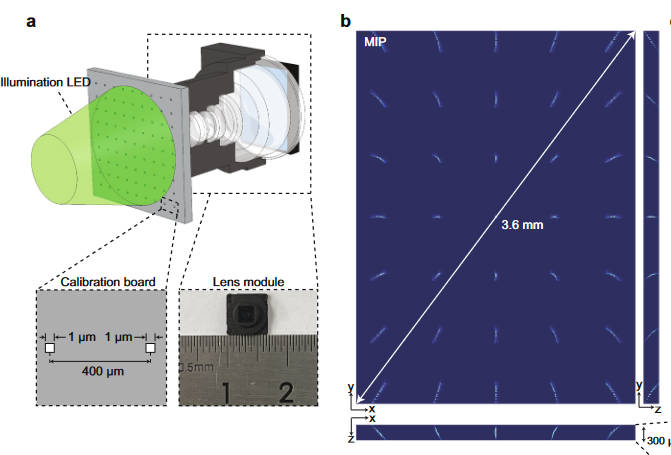
在PSF的标定方面很简单,用光刻技术直接在一块1mm厚的玻璃板子上刻了一系列1um的小孔,然后直接用镜头拍摄。
在如何对图片使用PSF卷积得到退化图像,本文建立了一个更细致的模型
由于相机系统拥有大FOV和大NA,导致PSF就更不像一个冲激函数了。为了解决这个问题,提出了一个考虑到PSF平移可变性的前向模型,并且优化了计算开销。假设具有平移可变性PSF的光学模型如下
\[i(x,y)=\sum_{u,v,z}s(u,v)p(u,v,x-u,y-v,z) \]
其中\((u,v)\)和\((x,y)\)分别是物平面和像平面的坐标,而\(z\)代表不同的深度,每个像\(s(u,v)\)都对应一个PSF矩阵,表示为\(p(u,v,x,y,z)\)。由上式也看得出来计算他要迭代所有PSF,复杂度很高,需要对其进行降维。作者这里的想法是进行矩阵分解,将PSF分成一系列基\(h_i(x,y)\)的加权和
\[p(u,v,x,y,z) = \sum^N_{i} w_i(u,v,z)h_i(x,y,z) \]
其中\(N\)是具有平移不变性的基\(h_i\)的个数。在实践上,对每个深度\(z\),都只标定一共\(M\)个PSF,最后得到一个PSF集合\(\{p(u,v,x_i,y_i,z)\},1\leq i\leq M\)。这些PSF经过下采样、剪裁、向量化,最后合并成一个矩阵\(\mathbf{P}\),同样的也有基矩阵\(\mathbf{H}\)和权重矩阵\(\mathbf{W}\),于是我们就可以通过数值方法估计\(\mathbf{H,W}\)
\[\mathbf{\hat H},\mathbf{\hat W}=\underset{\mathbf{H},\mathbf{W}}{\arg\min}||\mathbf{H}\times\mathbf{W}-\mathbf{P}||^2_2 \]
估计完成后,就可以将成像系统表示为
\[i(x,y,z)=\sum^N_{i=1}\sum_{u,v}s(u,v)w_i(u,v)h_i(x-u,y-v,z) \]
使用卷积表示则更简单
\[i(x,y)=\sum^N_{i=1}\{(s(u,v)\times w_i(u,v))\ast h_i(u,v)\}[x,y] \]
作者使用一个电动控制台和一个显微镜来获取训练数据。首先用显微镜在正好对上焦的位置拍摄一张图片(文中称作一个sample),然后在\([-150\mu m,150\mu m]\)的范围上以\(10\mu m\)为步长移动显微镜来拍摄,从而得到一系列配对的训练数据。
似乎本文提出的镜头在PSF标定和使用方面就只有上面这些内容。下面的部分似乎是用于效果对比,将本文的神经网络方法和传统的PSF去卷积方法对比。
TODO:有待补完,Deconvolution部分本文说的很模糊,并且疑似有公式错误。
A Physics-informed Low-rank Deep Neural Network for Blind and Universal Lens Aberration Correction
本文介绍了一种使用一组典型PSF来提取特征基,从而为畸变建模的方法。
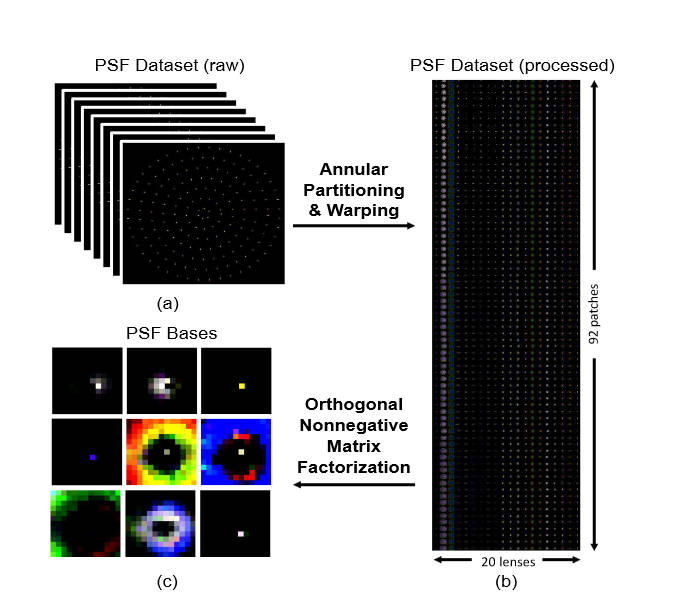
这里从Zemax里选出了20个PSF数据,因为PSF是具有旋转对称性的,于是又将一个平面上的PSF拆成多个同心圆环,然后再将圆环展开成长方形,将长方形前后拼合。最后将20个镜头的PSF长方形拼合起来得到一个矩阵,对其进行ONMF(正交非负矩阵分解)分解,得到一组基\(\{B_i\}\),之后所有的PSF都可以由下式表述
\[k=\sum_i\alpha_i\cdot B_i \]
图像退化过程就可以由下式表述
\[Y=X\ast(\sum_i\alpha_i\cdot B_i) + n = \sum_i(\alpha_i\cdot X)\ast B_i + n \]
其中\(X\)是锐利图像,\(Y\)是退化图象,而\(n\)是噪声。
我们同样可以将退化图象进行分解,分解出模糊成分\(\{Y_i=(\alpha_i\cdot X)\ast B_i\}\)。之后,我们就可以通过预训练的方式,训练一个去卷积模型,通过预测参数\(\alpha_i\)的值来消除像差。
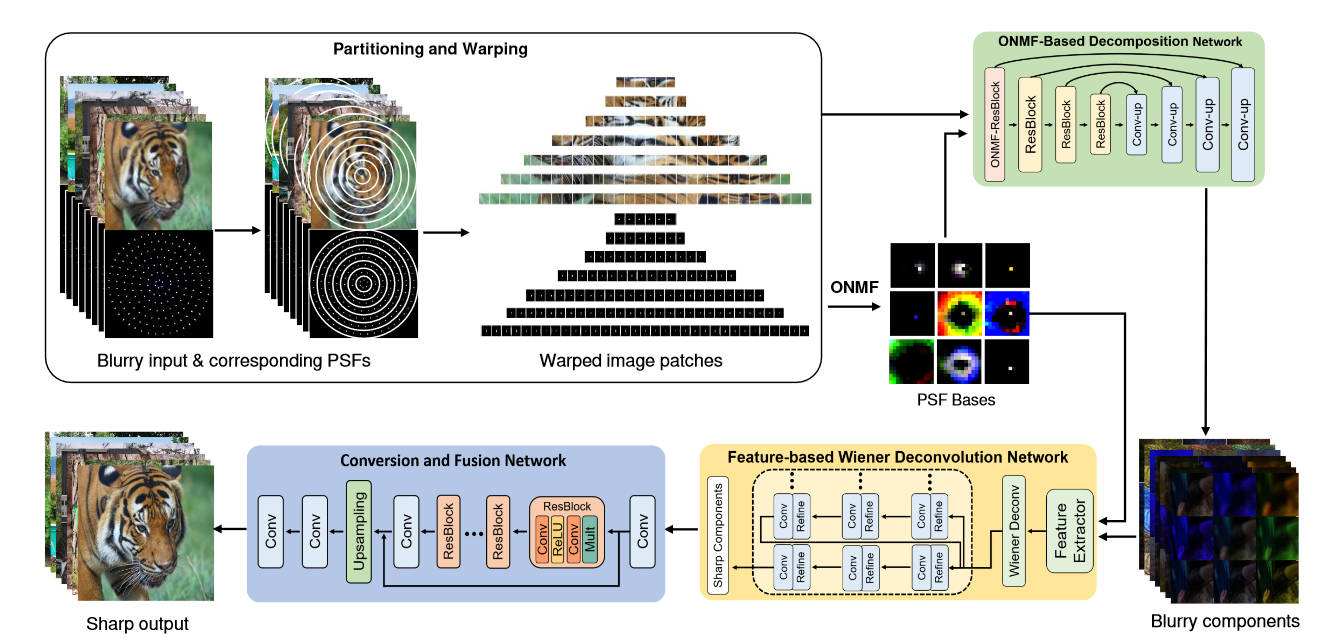
本文提出的方法主要分为三块。第一块负责将原图的模糊成分(特征)提取出来。
在训练过程中,使用Zemax及其中的PSF,来将一个锐利图像\(X\)合成出一个退化图象\(\tilde{Y_i}=X\ast(\alpha_i\cdot B_i)\),然后将退化图像\(\tilde{Y}\)和基\(B\)一起送进基于U-net的网络中,输出模糊成分\(Y_i\),使用的损失函数如下
\[\mathcal{L}_{decom} = ||Y-\sum_iY_i||_2+\sum_i(Y_i-\tilde{Y}_i) \]
其中第一项是为了让\(Y_i\)的加和和输入一样(我怀疑是不是符号有误),第二项是为了让每一项\(Y_i\)和合成的\(\tilde{Y}_i\)一样。
然后是第二部分,进行去卷积。本文提取出来的模糊成分和普通照片的特征区别挺大的,所以不能按常规的思路在空间域上进行去卷积,作者这里使用了在特征域上去卷积的方式。
\[X^*_i=\arg\min||Y_i-X_i\ast B_i|| \]
在实现上,作者使用了一个基于特征的自适应维纳滤波网络,设\(f_i\)是可学习的线性滤波器集合,和\(Y_i\)进行卷积来获得有用的特征,于是
\[F_iY_i=F_i(X_i\ast B_i)+F_in \]
这里的\(F_i\)是\(f_i\)的傅立叶变换(作者能不能统一一下大小写,其他的大写都是空间域的,只有\(F\)是频域的)。于是,我们的优化目标也就等价于寻找一个维纳滤波操作\(G_i\)来进行像差矫正
\[X_i^*=\arg\min||G_iF_iY_i-F_iX_i|| \]
最后误差函数是
\[\mathcal{L}_{deconv} = ||F_iX_i-G_iF_iY_i||_2 \]
这里我个人觉得作者说的很乱,作者的意思看图可能更容易理解。首先将模糊成分\(Y_i\)送进特征提取器,提取特征得到\(F_iY_i\),这个\(F_i\)似乎是可学习的,然后将其送入预训练的维纳滤波\(G_i\)中,这一部分是不可训练的。然后得到的\(G_iF_iY_i\)再经过一系列网络,输出了一个预测的\(\hat X_i\)。网络的目标是期望这个\(F_i\hat X_i\)和真实标注\(F_iX_i\)更接近。
目前来说将预估出来的\(X_i\)组合起来就得到了锐利图片,但事实上由于分解的不精确性和去卷积的伪影,最终会影响到图像质量。为此作者又提出了第三部分,基于注意力的混合模块。这个模块是一个可训练的网络,输入所有的锐利patch,输出一张完整的锐利的图。
Image restoration for optical zooming system based on Alvarez lenses
https://opg.optica.org/oe/fulltext.cfm?uri=oe-31-22-35765&id=540720
本篇解决了基于Alvarez镜头组的光学变焦系统的图像恢复问题,有很多光学设计的内容,不过我不懂,除去这一部分的话本文内容不多。
首先是获取配对数据,仍然是使用锐利图像,然后卷积上PSF得到退化图象。对于图像恢复部分,本文基于MIMO-UNet进行了修改
损失函数使用CharbonnierLoss
\[Loss=\sqrt{(output-input)^2+\epsilon^2} \]
Neural nano-optics for high-quality thin lens imaging
https://www.nature.com/articles/s41467-021-26443-0
本文针对超透镜进行校正。
本文将超透镜的设计融入到了训练过程中,超透镜的参数可由下式表述
\[\phi(r)=\sum^n_{i=0}a_i\left(\dfrac{r}{R}\right)^{2i} \]
由于笔者不是很清楚光学设计,所以就把这里简单当做一个函数,参数可调,场景用其获取能产生一些数值。
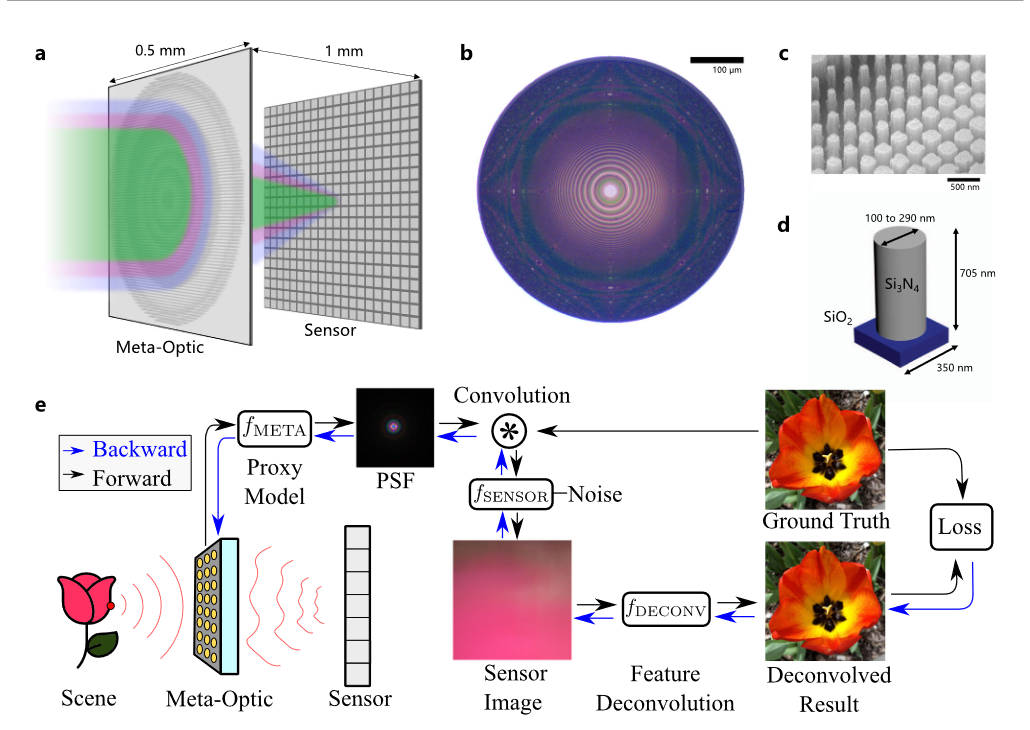
上图描述的是整个端到端的流程,其可以用下式表述
\[O=f_{\text{DECONV}}(P_{\text{DECONV}}, f_{\text{SENSOR}}(I\ast f_{\text{META}}(P_{\text{META}})), f_{\text{META}}(P_{\text{META}})) \]
其中\(P_{\text{META}}\)就是超透镜的参数,使用函数\(f_{\text{META}}\)计算出理论PSF,和输入信号进行卷积(在训练过程中是数据集的gt图像)。\(f_{\text{SENSOR}}\)模拟传感器的行为,其中包含了传感器的噪声。然后就是去卷积的神经网络\(f_{\text{DECONV}}\),其参数为\(P_{\text{DECONV}}\),接受传感器产生的图像,并且由于是非盲,也接受PSF,最终生成一张预测的清晰图像。损失函数就是gt和预测之间的L1损失。
在联合优化过后,就使用最优的超透镜参数去制造超透镜物理实体。
Realistic Image Degradation with Measured PSF
https://arxiv.org/abs/1801.02197
这篇文章虽然是反过来模拟像差的,但很多文章是用合成数据的,这篇文章也可以进行一定了解。
本文采集的PSF是用高精度仪器采集的,不是用我们之前说到的各种数值和深度学习方法,用的是单色滤镜,所以只有单通道的PSF。一共测试了27个镜头,有三个参数:离焦\(\Delta z\)、图像高度\(R\)、 方位角\(\phi\)。
由于这个测量的精度很高(0.3um),比传感器的像素尺寸(3um)小的多,所以可以进行下采样来提升效率。在本文中,下采样至大约6um的像素大小,得到一个13x13的PSF。
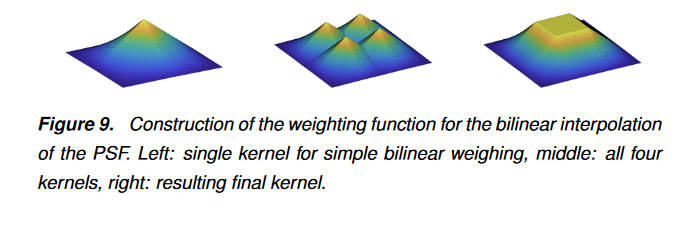
作者这里是想对每一个像素都卷积一个专属于它的PSF,从而达到比较好的结果。为此,作者将之前测量到的PSF作为gt,将\(\Delta z\)、\(R\)、\(\phi\)作为数据输入,让神经网络拟合出PSF。然后对每一个像素都预测一个PSF。但作者认为这又太麻烦了,PSF在短距离内变化不大,不如直接用插值的方法去弄。
上面的红点是有测量过PSF的位置,其他位置通过双线性插值得到。
之后使用插值的或真实的PSF对图像卷积就得到了退化图像,同时为了减小拍摄图像自带的退化,还对数据提前使用了盲去卷积。
但是在模拟退化的这个过程中,没有考虑到离焦距离\(\Delta z\),作者后面说了一大堆提出的PSF模型有\(\Delta z\)的好处,但我并没有看到和计算退化有什么关系,整篇文章都很乱。
End-to-end hybrid refractive-diffractive lens design with differentiable ray-wave model
https://dl.acm.org/doi/full/10.1145/3680528.3687640
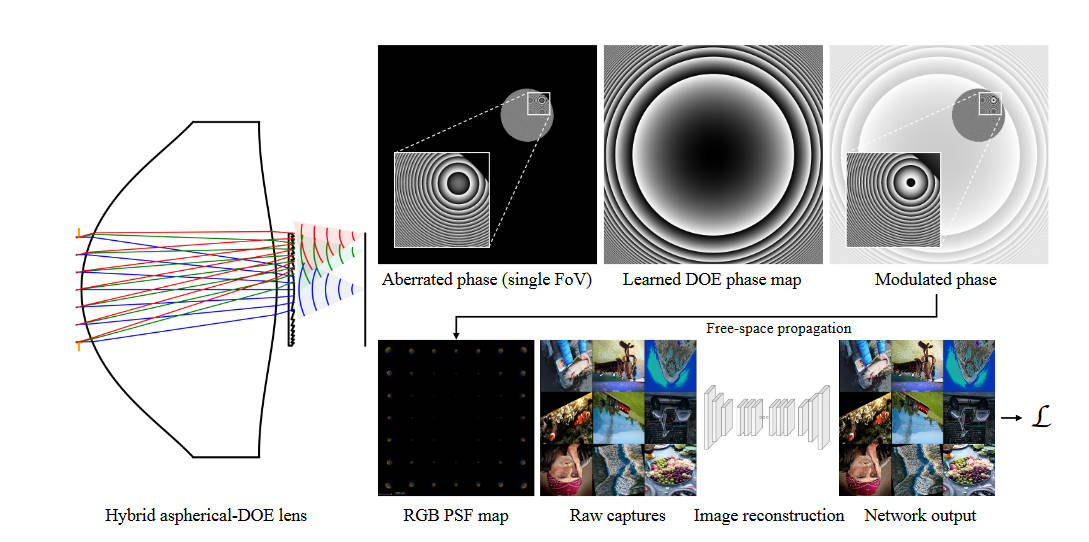
这篇文章首次提出一个可微分的、精度高的折射-衍射混合成像模型,来让镜头设计和神经网络结合在一起,从而能够端到端的进行训练。
同前,光学部分不是很懂,简要介绍一下提到的公式。
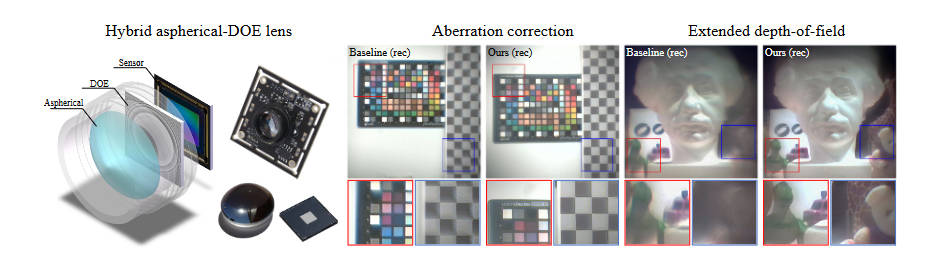
本文的镜头组如下图
他首先是一连串折射镜片,最后接上一个衍射镜片(衍射光学元件,DOE),然后再接到传感器上。在模拟这个镜头的物理性质时,使用了一种光线-光波结合的方法,在前面的折射镜片上使用光线追踪,而在后面的DOE上使用相位调制等方法去分析。
蒙特卡洛光线追踪的过程可以表示如下
\[\left\{\begin{matrix} \mathcal{I}_n(\mathcal S_n):(o^{n-1}, d^{n-1},\phi^{n-1},\lambda)\to (o^{n}, d^{n-1},\phi^{n},\lambda)\\ \mathcal{R}_n(\mathcal S_n):(o^{n}, d^{n-1},\phi^{n},\lambda)\to (o^{n}, d^{n},\phi^{n},\lambda) \\ (o,d,\phi,\lambda)=(\mathcal{R}_N\mathcal{I}_N\dots\mathcal{R}_1\mathcal{I}_1)(o^0, d^0, \phi^0, \lambda) \end{matrix}\right. \]
其中\(\mathcal{I}\)指的是光线与平面\(\mathcal{S}\)的相交,\(\mathcal{R}\)指的是光线在平面\(\mathcal{S}\)上的折射,\(o,d,\phi,\lambda\)分别是位置、角度、相位、波长。当计算完所有折射后,光线就抵达DOE前表面,此时可以计算光场为
\[U_{DOE^-}=\sum^{spp}_{i=1}u_i\exp(j\phi_i)\cos
其中\(u_i\)是振幅,\(\phi_i\)是光线\(i\)的相位,\(spp\)是蒙特卡洛采样的光线数,\(n\)是DOE表面的法向量。在DOE的调制过后,光场可以写为
\[U_{DOE^+}=U_{DOE^-}\exp\left(j\dfrac{n_\lambda-1}{n_0-1}\dfrac{\lambda_0}{\lambda}\phi_0\right) \]
计算完之后,我们就可以算出传感器表面的光场
\[U_{Sensor}=\mathcal{F}^{-1}(\mathcal{F}(U_{DOE^+})H) \]
其中\(H\)是传递函数,之后PSF计算如下
\[PSF=|U_{Sensor}|^2 \]
在实验中,作者计算了10x10个RGB PSF。同样,使用PSF来和图像卷积,构造出退化图像。之后使用NAFNet作为图像恢复模型,损失函数如下
\[\mathcal{L}=\mathcal{L}_{pixel}(\mathcal{N}(PSF\ast I), I) + \alpha\mathcal{L}_{percep}(\mathcal{N}(PSF\ast I), I) \]
其中\(I\)是输入图像,也被当做ground truth使用,\(\mathcal{N}\)代表着NAFNet,\(\mathcal{L}_{pixel}\)代表均方误差,\(\mathcal{L}_{percep}\)代表着VGG loss。
Grayscale to Hyperspectral at Any Resolution Using a Phase-Only Lens
https://arxiv.org/abs/2412.02798
这篇文章主要面向metalens的像差矫正。本文使用的相机由一个衍射元件和一个无滤镜的传感器组成,获取到多个波长的光线,输出的是一个加和的灰度图。本文的目标是从这个灰度图中恢复出31个通道的图像。使用的是一个conditional denoising diffusion model
一个高光谱图像(HSI),记作\(\mathbf{x}\in\mathcal{R}^{H\times W\times C}_{\geq 0}\),被传感器测量后变成单通道的\(\mathbf{y}\in\mathcal{R}^{H\times W}_{\geq 0}\),成像的过程为
\[\mathbf{y}(u,v)=\mathcal{M}(x)=\sum_\lambda o(\lambda)\cdot f(u,v,\lambda) \underset{(u, v)}{\ast} \mathbf{x}(u,v,\lambda) \]
其中\(f(u,v,\lambda)\)是PSF,\(\lambda\)是波长。\(o(\lambda)\)是传感器的光谱响应。于是对于高光谱图像的测量就变成了一个线性的编码过程,将3D的高光谱“体”编码成2D“图”。这里的PSF测量似乎不是本文的重点,根据附录来说PSF似乎是理论计算值,整个实验是在合成数据上进行的。
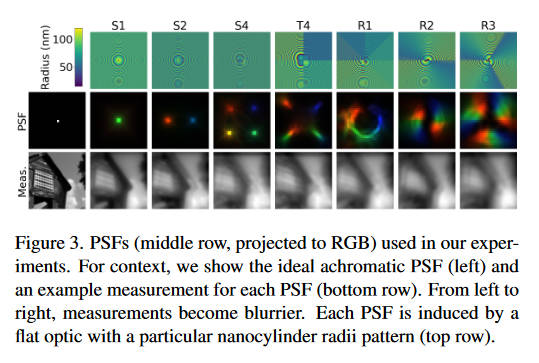
在本文的实验中使用了8个PSF,目的是为了测试哪种光学编码器(指的应该是衍射元件而非神经网络中的编码器)是最好的。左边的PSF较为稀疏,能够产生更锐利的图像,但是编码光谱信息的能力比右边的PSF弱。因为重建任务需要同时保持空间和光谱的高准确性,所以哪种PSF较好并不是很显然。
这上面的每一种PSF都可以通过设计合适的metalens来在物理上实现。我认为作者的逻辑应该是先用这八种PSF去测试,看哪种效果最好,然后依照最好的这个PSF来生产metalens。
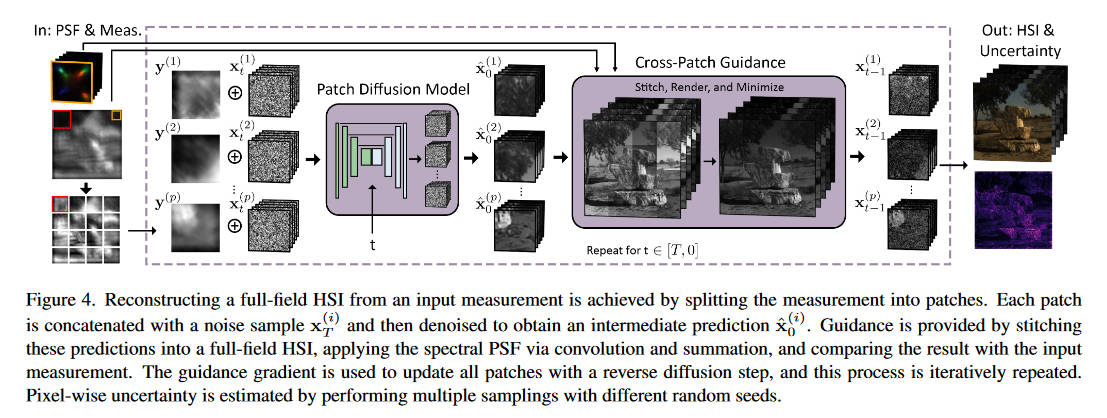
本文使用扩散模型来解决图像恢复问题,但并不是整张图上进行,而是分patch进行,作者说从实验结果上来看这样是更好的。
训练数据是从ARAD1K中获取的HSI,然后使用我们前面介绍的成像模型来合成退化图像,然后就得到了配对数据\((x_0^{(i)}, y^{(i)})\)。看起来作者意识到它的合成过程中,卷积计算涉及到了patch以外的信号,但是结果上来说影响不大。
同上图介绍的,往扩散模型中添加condition是通过将\(x,y\)拼在一起实现的,然后让模型在每一步的中间都输出一个预测的HSI\((\hat{\mathbf{x}}^p_0)\),再将他们拼成一张大图,使用前述成像过程进行一次退化,让它的结果和真实标签\(y\)一致,作者说用这个方法引道全局的去噪过程。如下
其中上标\(p\)代表patch,\(Stitch\)代表这个拼图的过程,\(\mathcal{M}\)就是前面的成像过程。由于\(y\)和\(x_0\)是max-normalized的,所以模型预测出来的HSI是带有一个未知的比例因子的,为了校正这个比例因子,多了一步过程,也就是这个cross-patch guidance。
(上图有误,应该是\(\arg\min\))将\(\hat x\)乘以一个因子再拼起来,然后经过成像模型退化,尽量和标签\(y\)一致,取这个最好的因子\(c\),再取和标签的误差,作为优化\(x_t\)的误差。将\(x_t\)优化后再放入扩散模型的去噪过程中。
最后按照这个模型走\(T\)步去噪过程,就得到了最终预测的HSI。作者将光谱的不确定性量化如下
\[\text{Uncertainty} = \sum_{\lambda}\text{Var}(\{\mathbf{x}_0\}^N_{i=0}) \]
一共预测了\(N\)次。
Achromatic Single Metalens Imaging viaDeepNeural Network
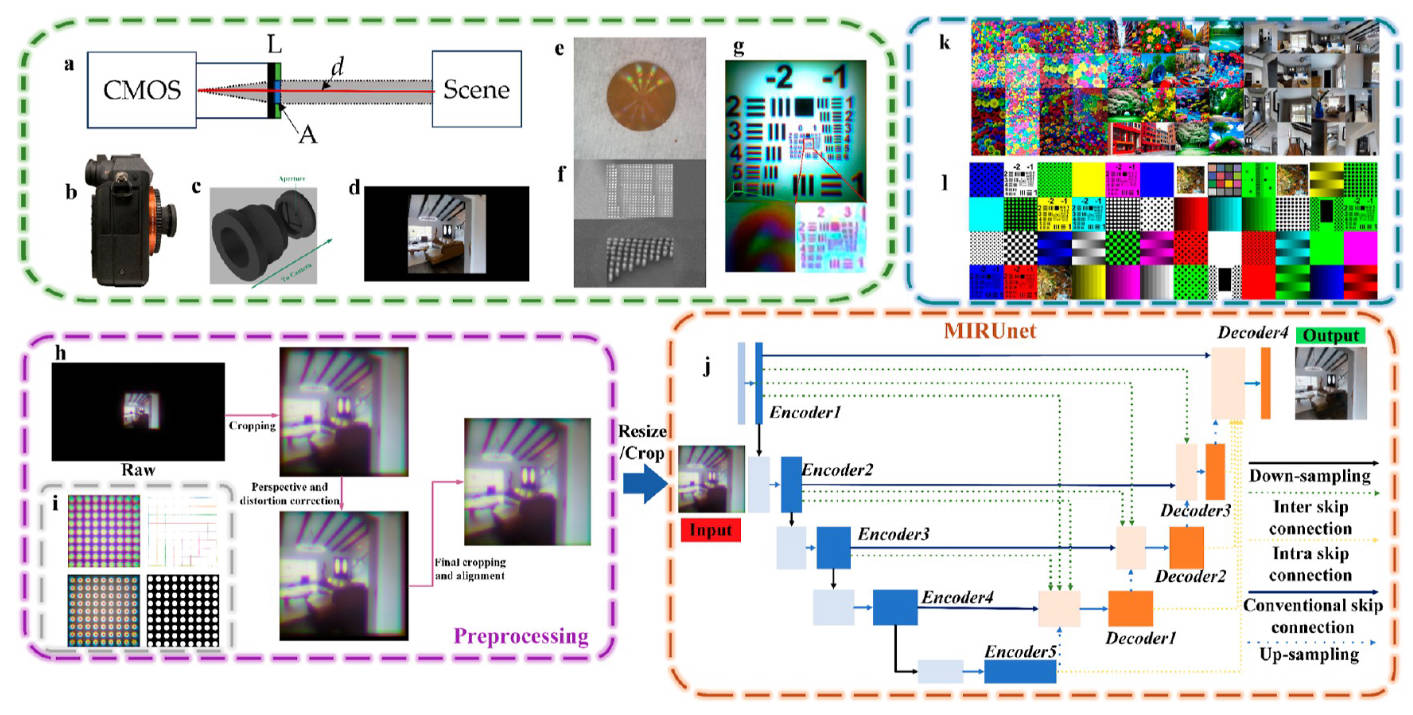
本文也是针对metalens进行像差矫正,但是没有引入PSF数据。模型没什么特别的,主要关注一下成像模型和数据获取方式。
首先介绍一下本文使用的成像模型
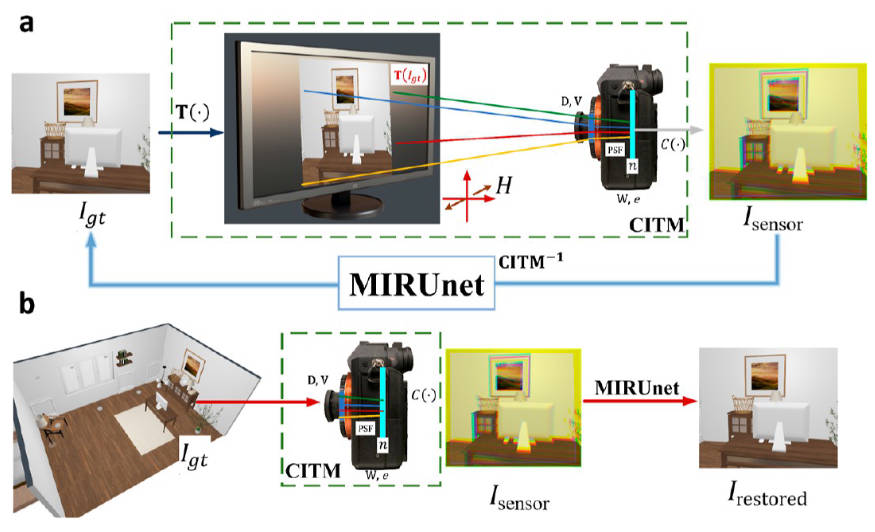
\[I_{sensor} = C(\mathbf{w}\cdot\mathbf{v}\cdot e\mathbf{D}(T(I_{gt}(\lambda))_{H^{-1}}\ast PSF(\lambda))+n) \]
其中\(I_{sensor}\)是相机获取到的图像,\(I_{gt}(\lambda)\)是真实图像的该波长下的分量,\(T\)指的是一个转换函数,将gt图像转化成显示屏上的图像。相机获取的一部分数据实际上是对着显示屏拍。
\(PSF(\lambda)\)是在该波长下的PSF,\(\ast\)是卷积,\(\mathbf{W}\)是色彩平衡矩阵,\(\mathbf{V}\)代表晕影,\(H\)代表透视投影矩阵,\(D\)代表镜头畸变,\(e\)是曝光参数,\(n\)是噪声,\(C\)是剪裁函数,剪裁最大最小信号值。
本文是盲去卷积,没有使用测量的PSF。作者认为是metalens的测量比较困难,而且和波长相关,并且PSF通常还不是uniform的。
上面的成像模型很全面,但是本文主要只关注彩色图像的质量增强,于是就只保留了\(\mathbf{w},\mathbf{v},PSF\)这三项,其他的项在数据采集的过程中去除。其中,曝光参数的去除是通过手动设定相机曝光实现的。镜头畸变和透视投影是通过拍摄test charts来去除的。去除过程见上图h部分。gt到显示器的转移矩阵是通过校正显示器去除的。
可以从上图的g部分看到有效性,矫正过的图片在几何上和gt高度相似,在雾状退化、分辨率降低等方面就证实了我们只剩下前述的3项需要矫正。
矫正就没什么好说的,UNet一把抓。损失函数是
\[\mathcal{L}=\alpha L_{Perceptual}+\beta L_{PSNR} \]
\[L_{Perceptual}=\sum^n_{i=m}\beta_il_{p_i}(I_{gt}, I_{restored}) \]
\[l_p(I_{gt}, I_{restored}) = ||P(I_{gt})-P(I_{restored})||^2 \]
\(P(\cdot)\)指的是预训练的VGG19,\(i\)是指模型的第\(i\)个卷积层。
\[L_{PSNR} = \dfrac{1}{(10\log 10((I_{max}^2)/MSE(I_{gt}, I_{restored})))} \]