线段光栅化算法
从《Fundamentals of Computer Graphics》(第五版)中的第179页,我们得到了一种直线的表达方式,
\[f(x,y)\equiv (y_0-y_1)x+(x_1-x_0)y + x_0y_1-x_1y_0 = 0 \]
其中\((x_0,y_0),(x_1,y_1)\)代表直线上的任意不同的两点。并且\(x_0\leq x_1\),如果这个不满足,就交换两点的序号。然后直线的斜率显然就是
\[m = \dfrac{y_1-y_0}{x_1-x_0} \]
方便起见,我们先假设\(m\in(0,1]\)。
显然,我们要画一条直线的话,无非就两种情况:
要么向右移动一格,要么向右后再向上移动一格。总之,我们总是向右移动一格,然后根据某种条件向上移动一格。我们可以把这个条件设置为
\[\mathbf{if}\ f(x+1,y+0.5)<0\ \mathbf{then}\ y=y+1 \]
注意这里的\((x,y)\)取整数,起始像素在直线上。
进一步的,如果我们不想每次都调用函数\(f\),我们有如下优化
y = y0
d = f(x0+1,y0+0.5)
for x = x0 to x1 do
draw(x,y)
if d<0 then
y = y+1
d = d+(x1-x0)+(y0-y1)
else
d = d+(y0-y1)
不优化的方法写成cpp的样子大概如下
if(p0->x>p1->x) std::swap(p0,p1);
auto fxy = [&](float x, float y)->float{
return (p0->y-p1->y)*x+(p1->x-p0->x)*y+p0->x*p1->y-p1->x*p0->y;
};
int y = p0->y;
for(int x = p0->x ; x<=p1->x ; x++){
image.setFragment(x,y,color);
float er = fxy(static_cast<float>(x)+1.f, static_cast<float>(y)+.5f);
if(p0->y<p1->y && er<0.f && y<image.getHeight()-1){
y++;
}
else if(p0->y>p1->y && er>0.f && y>0){
y--;
}
}
这里写的包括了\(m\in[-1,1]\)的情况,负数情况很简单,就把y++变成y–,以及判断小于零转变为判断大于零。
当\(m\in(1,+\infty]\)时,情况转变为,我们要么向上走一格,要么向上后向右走一格,与之前的情况非常相似,我们只要把遍历x改成遍历y,判断x++的条件即可。
三角形光栅化算法
我会直接使用三角形的重心坐标来实现三角形的光栅化,因为比起其他一些扫描方法,重心坐标能比较方便的实现插值。
三角形的重心坐标可见《Fundamentals of Computer Graphics》(第五版)中的第52页。
根据线性代数的知识,假设我们三角形有三个不重合的点\(A,B,C\),则我们可以用\(\vec{AB},\vec{AC}\)表示平面中任意的点\(p\),我们有如下公式
\[\vec{p} = \alpha\vec{a} + \beta\vec{b}+\gamma\vec{c} \]
其中\(\alpha+\beta+\gamma=1\)
可以计算得到,对于平面上的任意一个点\((x,y)\)
\[\gamma = \dfrac{(y_a-y_b)x+(x_b-x_a)y+x_ay_b-x_by_a}{(y_a-y_b)x_c+(x_b-x_a)y_c+x_ay_b-x_by_a} \]
\[\beta = \dfrac{(y_a-y_c)x+(x_c-x_a)y+x_ay_c-x_cy_a}{(y_a-y_c)x_b+(x_c-x_a)y_b+x_ay_c-x_cy_a} \]
\[\alpha = 1-\beta-\gamma \]
当这个点在三角形内时,满足以下条件
\[0<\alpha<1 \]
\[0<\beta<1 \]
\[0<\gamma<1 \]
特别的,如果在三角形上,则可以取等号。总体还是要满足\(\alpha+\beta+\gamma=1\)。
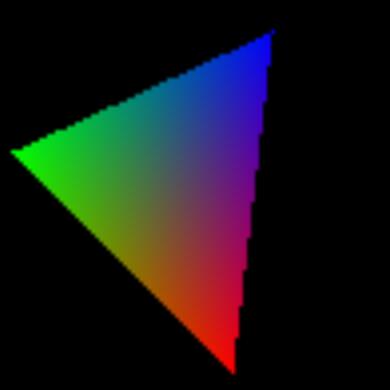
这个东西好就好在,如果需要对颜色进行插值,对于三角形内部任意一点\(p\),有\(color_p=\alpha color_a+\beta color_b+\gamma color_c\)。
我们绘制的时候设置三个点为红、绿、蓝,中间颜色进行插值,就会得到这个结果
接下来我们谈谈具体怎么画三角形。
首先非常暴力的想法是,把整个屏幕上的点扫描一遍,如果这个点在三角形内部,就给他上色。
稍微优化一下,我们只需要扫描三角形的外接矩形(四边平行于坐标轴)即可。
cpp代码如下
int maxx = 0, minx = image.getWidth()-1, maxy = 0, miny = image.getHeight()-1;
for(int i=0;i<3;i++){
maxx = std::max(maxx, points[i].x);
minx = std::min(minx, points[i].x);
maxy = std::max(maxy, points[i].y);
miny = std::min(miny, points[i].y);
}
for(int x=minx;x<=maxx;x++){
for(int y=miny;y<=maxy;y++){
std::tuple<float,float,float> ret = geo::getBarycentric(points, x, y);
float alpha = std::get<0> (ret);
float beta = std::get<1> (ret);
float gamma = std::get<2> (ret);
if(0.f<=alpha && alpha<=1.f &&
0.f<=beta && beta <=1.f &&
0.f<=gamma && gamma<=1.f)
{
geo::OARColor color = static_cast<geo::vec4i>(
alpha*static_cast<geo::vec4f>(colors[0]) +
beta*static_cast<geo::vec4f>(colors[1]) +
gamma*static_cast<geo::vec4f>(colors[2]));
image.setFragment(x,y,color);
}
}
}
全部光栅化的代码可见**这里**
另外,求重心坐标的代码我写到了geometry.cpp里,方便别处调用。链接在**这里**(在文件末尾)
另外,求重心坐标还有一种不那么复杂的公式,见**计算机图形学基础学习笔记-数学基础**
注意,
if(0.f<=alpha && alpha<=1.f &&
0.f<=beta && beta <=1.f &&
0.f<=gamma && gamma<=1.f)
这一段代码也可以写作
if(alpha < 0.f || beta < 0.f || gamma < 0.f) continue;
这也是对的。唯一需要小心的是精度问题,float的精度可能不足以把边界上的每一个点都画出来。如果你不在乎这一两个像素点就可以不用管,如果你在乎,那么我们可以修改为alpha<-(1e-5)这样的条件。
使用例子
绘制线段
#include "tga_image.h"
#include "raster.h"
int main(){
TGAImage image(100,100,TGAType::rgb);
geo::vec2i pts0[2] = {geo::vec2i(99,0),geo::vec2i(0,99)};
ras::line(image, pts0, geo::OARColor(255,0,0,255));
for(int i=0;i<=99;i+=10){
pts0[0] = geo::vec2i(i,0);
ras::line(image, pts0, geo::OARColor(255,0,0,255));
}
image.writeToFile("./line.tga");
}
如上,我们首先绘制了一条\((99,0),(0,99)\)的直线,也就是从右下角到左上角,然后我们用循环绘制了一组,一个点固定在右上角的直线。
效果如下
绘制三角形
#include "tga_image.h"
#include "raster.h"
int main(){
TGAImage image2(100,100,TGAType::rgb);
geo::vec2i pts1[3] = {geo::vec2i(60,5),geo::vec2i(5,60),geo::vec2i(70,90)};
geo::OARColor colors[3] = {geo::OARColor(255,0,0,255),geo::OARColor(0,255,0,255),geo::OARColor(0,0,255,255)};
ras::triangle(image2,pts1,colors);
image2.writeToFile("./triangle.tga");
return 0;
}
代码非常直观,就是把三个点和三个点的颜色设置一下扔到光栅化函数里去。效果如下