数制和编码
十进制、二进制、八进制、十六进制及其转换
过于简单,不多介绍。可以在计组笔记里找到
反码、补码和补码运算
也可以在计组笔记中找到。
十进制代码
每四位二进制对应一个十进制数。
主要有8421(BCD)、2421、5211、余3码、余3循环码。
8421,2421,5211是三种恒权代码,另外两个不是。
其中余3码就是在BCD码上加\(3\)得到的。余3循环码的特点是相邻的两个代码之间仅有一位状态不同。至于余3循环码怎么得到,看格雷码
需要注意的是他们的禁止码是哪些,在后面的时序逻辑电路可能会用到。按照从小到大的顺序写出\(0\sim 9\)对应的码,没写出来的就是禁止码。为什么要从小到大?比如2421码,最高位和第二低位都是2,我们要优先选择低位的。
格雷码
格雷码的形式如下,假设为四位格雷码,最开始是0000. 则最右边的一位变化为0110的顺序,第二位为00111100的顺序,第三位为0000111111110000.以此类推。注意第四位只循环了半个周期,四位格雷码就表示完毕了。
格雷码的特点是相邻的两个代码之间只有一位发生变化。在代码转换的过程中不会产生过渡噪声。
四位余3码就是从第四个格雷码开始取10个,即从0010开始到1010。
ASCII码
略。
逻辑代数基础
三个基本运算
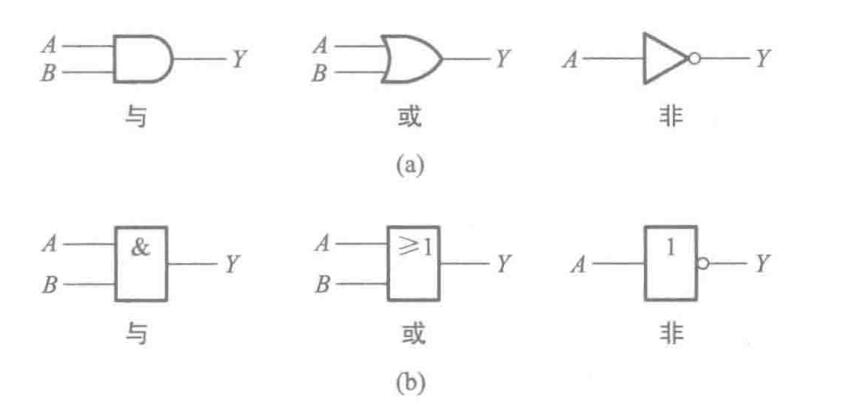
分别是与(AND)\((\cdot)\)、或(OR)\((+)\)、非(NOR)\(('或\overline{ })\),电路符号如下
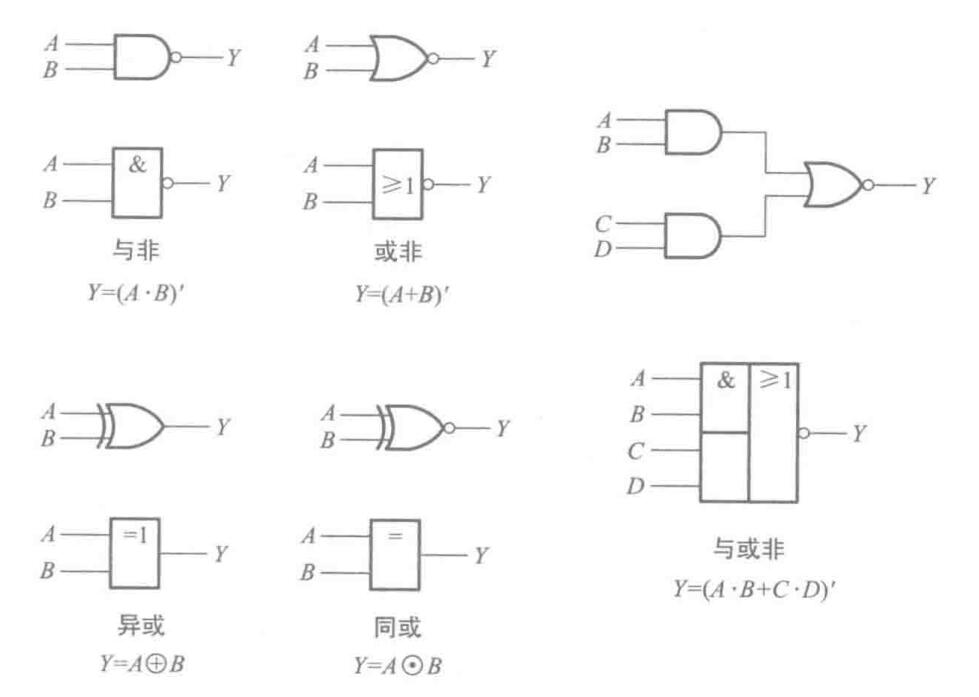
当然,这三个运算可以复合出一些操作。与非(NAND)、或非(NOR)、与或非(AND-NOR)、异或(XOR),同或(XNOR)。符号如下
其中异或有
\[A\oplus B = A\cdot B'+A'\cdot B \]
同或有
\[A\odot B = A\cdot B + A'\cdot B' \]
二者互为反运算,\(A\oplus B = (A\odot B)',A\odot B=(A\oplus B)'\)
注意,与运算可以把\(A\cdot B\)写为\(AB\)。关于运算优先级,虽然书上没说,但是应该是非>与>或。
逻辑代数的基本公式和常用公式
要证明这些公式,可以列真值表。然后这些公式就可以用来证明别的公式了,比如下面的。
逻辑代数的基本定理
代入定理
在任何一个包含变量A的逻辑等式中,若以另外一个逻辑式代入式中所有A的位置,则等式仍然成立。
反演定理
对于任意一个逻辑式\(Y\),若将所有的\(\cdot\)换成\(+\),所有的\(+\)换成\(\cdot\),\(0\)换成\(1\),\(1\)换成\(0\),原变量换成反变量,反变量换成原变量,得到的结果就是\(Y'\)。
需要注意:
- 要保留原来的运算顺序,例如原来\(A+BC\),变换后要变成\(A'(B'+C')\)
- 不属于单个变量上的反号应保持不变,例如\((AC)'\)变换为\((A'+C')'\)
对偶定理
若两个逻辑式相等,则它们的对偶式也相等。
对偶式是:对于任意一个逻辑式\(Y\),若将所有的\(\cdot\)换成\(+\),所有的\(+\)换成\(\cdot\),\(0\)换成\(1\),\(1\)换成\(0\),得到的结果就是\(Y^D\)。
想要证明两个逻辑式相等,可以转换为证明它们的对偶式相等。有时候这更简单。
完备集
对于一个代数系统,若仅用它所定义的一组运算符号就能解决所有的运算问题,则称这一组符号是一个完备的集合,简称完备集。
对于逻辑代数,与、或、非毫无疑问是一个完备集。但它并不是最小的。与非、或非、与或非,它们三个都是能够单独组合实现与、或、非功能的。它们是最小的完备集。
逻辑函数
如果以逻辑变量作为输入,以运算结果作为输出,那么当输入变量的取值确定之后,输出的取值便确定了,因此输入输出之间是一种函数关系。
\[Y = F(A,B,C,\cdots) \]
常用形式
- 与或式。\(F=AB+CD\)
- 或与式。\(F=(A+B)(C+D)\)
- 与非与非式。\(F=\overline{\overline{AB}\cdot\overline{CD}}\)
- 或非或非式。\(F=\overline{\overline{A+B}+\overline{C+D}}\)
- 与或非式。\(F=\overline{{AB}\cdot{CD}}\)
任何逻辑函数都能转换成以上五种形式。它的作用在于,如果电路元件只给你某某元件,你要把原来的表达式转换为上述五种式子,再去套用元件。多用德摩根律。
描述方法
- 真值表
- 逻辑函数式
- 逻辑图(电路图)
- 波形图
两种标准式
最小项
\(n\)个变量的最小项\(m\)是含\(n\)个变量的“乘积项”,其中每个变量都以原变量或反变量的形式出现恰好一次。
\(n\)个变量的最小项有\(2^n\)个。
输入变量的每一组取值都使一个对应的最小项等于\(1\)。为了方便,例如\(A=1,B=0,C=1\)时,该最小项写作\(AB'C\)。如果看成二进制数\(101\),则最小项标记为\(m_{101}=m_5\)
最小项的性质有
- 在输入变量的任何取值下必有一个最小项,且仅有一个最小项的值为\(1\)
- 全体最小项的和为\(1\)
- 任意两个最小项的乘积为\(0\)
- 具有相邻性的两个最小项之和可以合并成一项并消去一对因子
最大项
\(n\)个变量的最大项\(M\)是含\(n\)个变量的“和”,其中每个变量都以原变量或反变量的形式出现恰好一次。
\(n\)个变量的最小项有\(2^M\)个。
与最小项正好相,反输入变量的每一组取值都使一个对应的最大项等于\(0\)。\(A=1,B=0,C=1\)时最大项写作\(A'+B+C'\),记作\(M_{101}=M_5\)
最大项的性质有
- 在输入变量的任何取值下必有一个最大项,且仅有一个最大项的值为\(0\)
- 全体最大项的积为\(0\)
- 任意两个最大项的和为\(1\)
- 只有一个变量不同的两个最大项的乘积等于各相同变量之和
最后,可以发现\(M_i=m_i'\)
逻辑函数的最小项之和形式
首先将给定的逻辑函数式化为若干乘积项之和的形式,亦称“积之和”形式。然后,再利用基本公式\(A+A'=1\)将每个乘积项中缺少的因子补全,这样就可以将与或的形式化为最小项之和的标准形式。
例如
\[Y = ABC'+BC \]
\[Y = ABC'+(A+A')BC = ABC'+ABC+A'BC=m_3+m_6+m_7 \]
也可以写作
\[Y(A,B,C)=\sum m(3,6,7) \]
### 逻辑函数的最大项之积形式
利用公式\(AA'=0\)
例如
\[Y = A'B+AC = (A'B+A)(A'B+C) = (A+B)(A'+C)(B+C) \]
\[Y = (A+B+CC')(A'+BB'+C)(AA'+B+C) = (A+B+C)(A+B+C')(A'+B+C)(A'+B'+C) \]
\[Y(A,B,C,D) = \prod M(0,1,4,6) \]
或者,我们可以先求\(Y'\),并且写出\(Y'\)的最小项,再把\(Y'\)求反得到最大项。或者得出\(Y\)的最小项,利用\(m_i\)和\(M_i\)的互补关系直接写出结果。
互补关系指的是,例如\(3\)个变量的表达式,\(Y\)最小式之和为\(\sum m(0,1,4,5)\),则\(Y\)最大项之积为\(\prod M(2,3,6,7)\),把剩下没用的都放到最大项里了。这个的证明可以在离散数学笔记中找到。
逻辑函数的化简
公式化简法
- 并项法,使用\(AB+AB'=A\)
- 吸收法,使用\(A+AB=A\)
- 消项法,使用\(AB+A'C+BCDE = AB+A'C\)
- 消因子法,使用\(A+A'B = A+B\)
- 配项法,使用\(A+A=A,A+A'=1\)
卡诺图法
介绍不方便,看教材。
注意事项:横轴和纵轴是格雷码排列的。但是填进去的时候,按照坐标的字面量填入最小项。而不是什么转换为格雷码对应的十进制数,再填入对应的十进制表示的最小项。
如果表达式里有这一项,就填入1,没有就填入0。例如有\(ABCD\)就填入坐标为\(11,11\)的那一格,也就是第三行第三列,填入\(m_{15}\),填入\(1\),没有这一项就填入\(0\)
如果你得到的是最大项,那么在卡诺图对应的位置填入\(0\),其他位置填入\(1\)。
合并规律
用尽可能大的圈,去套\(1\),不可套\(0\),但是可以重叠(不要多余,每个圈里面至少有一格只被套过一次)、可以越过边界到达相对的边界一边。
不方便说,多做题。
具有无关项的逻辑函数及其化简
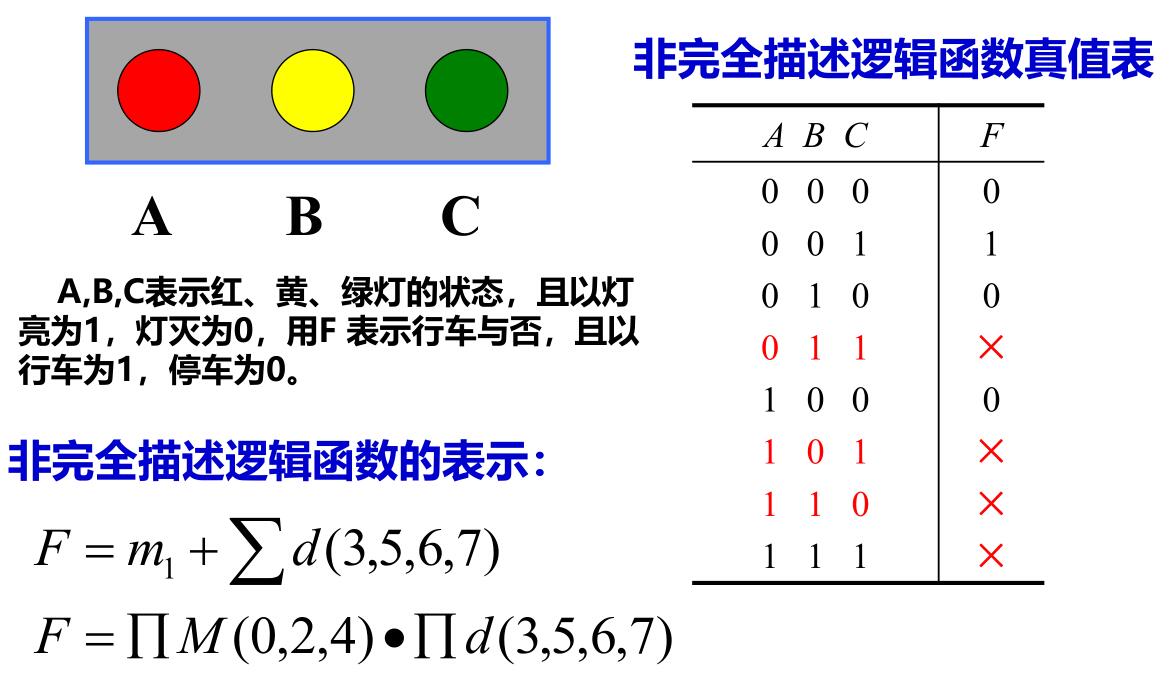
对于输入变量的每一组取值组合,逻辑函数都有确定的值,则这类逻辑函数称为完全描述的逻辑函数。
对于输入变量的某些取值组合,逻辑函数值不确定(可以为1,也可以为0),或者不存在,这类逻辑函数称为非完全描述的逻辑函数。
无关项在卡诺图里填\(\times\),在真值表里填\(\times\),在逻辑函数中用约束项表示
在逻辑函数中,一般最小项的约束条件为\(\sum d(\cdots) = 0\)。最大项的约束条件为\(\prod d(\cdots) = 1\)
在卡诺图化简中,带有\(\times\)的可以圈也可以不圈。
组合逻辑电路
概述
数字电路可以分为两类:组合逻辑电路、时序逻辑电路
组合逻辑电路的输出仅仅取决于该时刻的输入。
输入输出关系可以表示为
\[\left\{\begin{matrix} y_1=f_1(a_1,\cdots,a_n) \\ y_2=f_2(a_1,\cdots,a_n) \\ \vdots \\ y_m=f_m(a_1,\cdots,a_n) \end{matrix}\right. \]
写成向量形式为\(Y=F(A)\)
分析方法
根据电路图写表达式、列真值表,判断功能
设计方法
把想做的功能抽象出来,写成表达式,化简表达式,画电路图。
常用组合逻辑电路模块
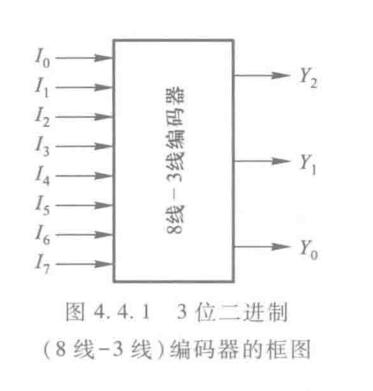
8-3普通编码器
功能就是,把某一位输入变成二进制位输出,比如\(I_6=1\),则输出\(110\)。
它普通就普通在,任意时刻只允许一个输入。
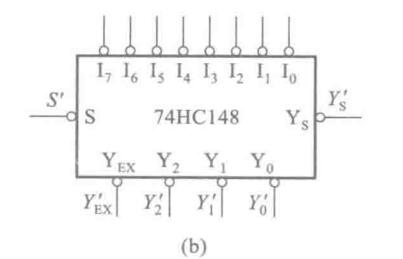
8-3优先编码器
可以有多个输入,但是按照内部的优先级顺序,会进行选择什么输出。注意这些圆点代表非门,或者说低电平有效。
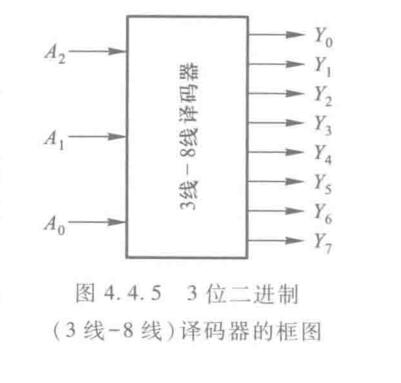
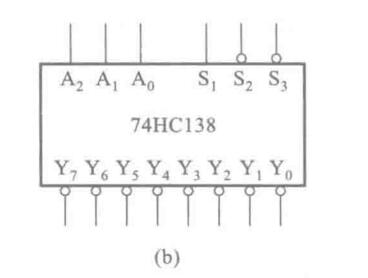
3-8译码器
就是8-3编码器反过来
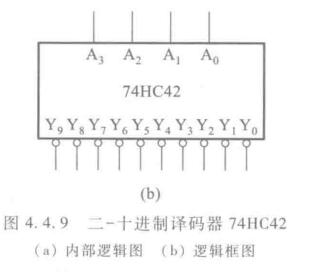
2-10进制译码器
也就是BCD翻译为10进制数字
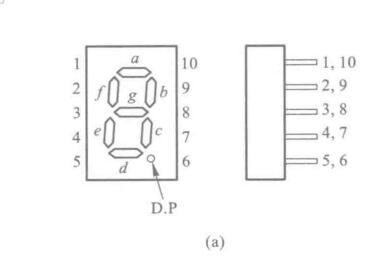
七段字符管
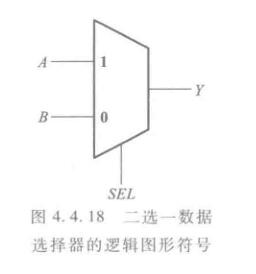
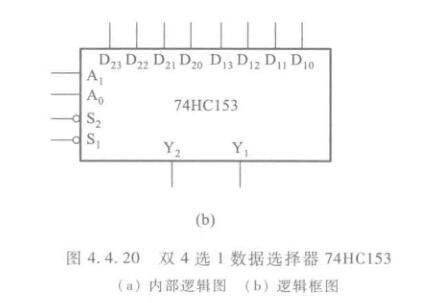
数据选择器
从一组输入中选出一个进行输出。
加法器
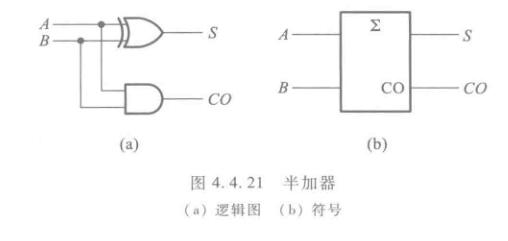
一位半加器
\[\left\{\begin{matrix} S = A'B+AB' = A\oplus B \\ CO = AB \end{matrix}\right. \]
不考虑低位的进位,称为半加。 \(S\)为本位加的结果,\(CO\)为进位
一位全加器、串行加法器、超前进位加法器
见计组笔记。
\[\left\{\begin{matrix} S = A\oplus B\oplus CI \\ CO = AB + (A\oplus B)CI \end{matrix}\right. \]
组合逻辑电路中的竞争-冒险
在组合电路中,某一输入变量经不同途径传输后,到达电路中某一会合点的时间有先有后,这种现象称为竞争。由于竞争而使电路输出发生瞬时错误的现象称为冒险。
将门电路两个输入信号同时向相反的逻辑电平跳变的现象称为竞争。
应当指出,有竞争不代表一定会产生尖峰脉冲。
判断有无竞争
只要输出端的逻辑函数在一定条件下能化简成
\[Y = A+A'\quad or\quad Y = AA' \]
则一定有竞争。
例如\(Y=AB+A'C\),在\(B=C=1\)时有\(Y=A+A'\)
或者在卡诺图上看。如果两卡诺圈相切,而相切处未被其他卡诺圈包围,则有竞争。
两个输入变量以上的竞争就难以判断了,最有效的办法是做实验。利用示波器观察,如果有毛刺,就有冒险。
消除竞争-冒险的方法
- 接入滤波电容
- 引入选通脉冲
- 修改逻辑设计
修改逻辑设计需要增加冗余项。
例如,\(Y = AB+A'C = AB+A'C+BC\),此时,当\(B=C=1\)时,无论\(A\)取什么值,都有\(Y=1\)
半导体存储电路
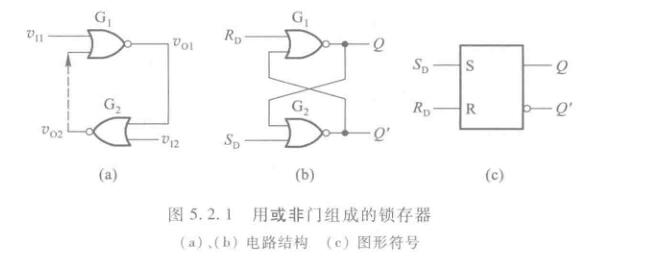
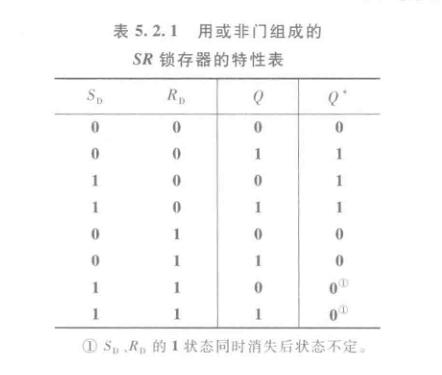
SR锁存器
注意我们约定不同时给SR输入有效。有些地方的SR锁存器是低电平有效,无论什么情况,记住:两个都无效时,保存原有的输出。S(Set)有效时,输出变为\(1\),R(Reset)有效时,输出变为\(0\)。
触发器
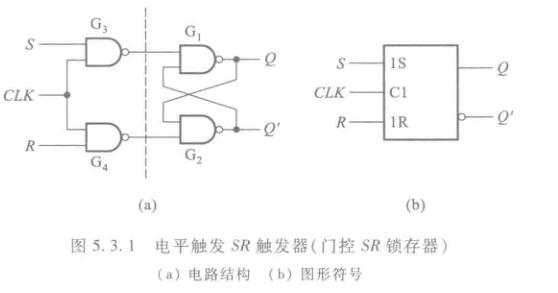
电平触发
- 只有当CLK为有效时,触发器才接受输入信号
- 在CLK=1的全部时间里,SR状态的变化都有可能引起输出状态的改变。在CLK回到0之后,触发器保存的是CLK回到0之前瞬间的状态。
显然,如果CLK=1时SR多次变化,输出也会多次变化。抗干扰能力弱。
边沿触发
触发器的次态仅取决于时钟信号的上升沿(或者下降沿)到达时的逻辑状态。抗干扰能力强。
脉冲触发
当CLK的有效电平消失以后,输出状态才改变。所以也叫延迟触发。
SR触发器
\[\left\{\begin{matrix} Q^* = S+R'Q \\ SR = 0(约束) \end{matrix}\right. \]
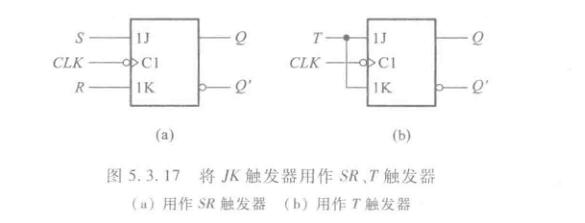
JK触发器
\[Q^* = JQ' + K'Q \]
也就是\(J=K=0\)时,输出不变,\(J=1,K=0\)时输出变\(1\),\(J=0,K=1\)时输出变\(0\),\(J=K=1\)时,输出翻转。
只是比SR多了一个翻转的功能而已。
由于JK可以实现SR和T,所以现在一般生产JK触发器和D触发器较多。
注意到上面的时钟信号输入端口有个三角形,和之前的不一样。之前没有三角形的代表电平有效,这里有三角的代表上升沿有效。如果还有个非门在前面,则代表下降沿有效。这张图的JK触发器是下降沿有效。
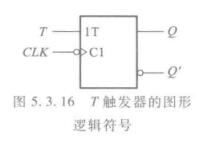
T触发器
\[Q^* = TQ'+T'Q \]
也就是说\(T=0\)时保持,\(T=1\)时翻转。
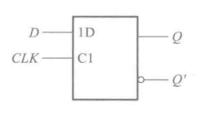
D触发器
\[Q^*=D \]
也就是说输出等于输入。
触发器功能的描述方法
- 状态转移真值表
- 次态卡诺图与特征方程
- 状态转移图
- 激励表
- 波形图
时序逻辑电路
概述
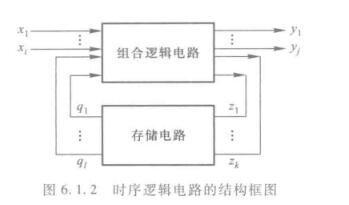
写成向量形式得到
\[Y = F(X,Q) \]
\[Z = G(X,Q) \]
\[Q^* = H(Z,Q) \]
第一个方程称为输出方程,第二个为驱动方程,第三个为状态方程。
在时序电路中区分出同步时序电路和异步时序电路。由于课时问题,我们学院只讲同步时序。
根据输出信号的特点分为米利型和穆尔型。米利型:输出信号取决于存储电路和输入变量。穆尔型:输出电路仅仅取决于存储电路。
分析方法
- 从给定的逻辑图中写出每个触发器的驱动方程
- 驱动方程代入相应触发器的特性方程,得出每个触发器的状态方程,从而得到状态方程组
- 根据逻辑图写出输出方程
表示方法
- 状态转换表
- 状态转换图。输入写斜线上,输出写斜线下,没有输入就空着。
- 状态机流程图
可自启动电路
时序电路中的所有无效状态经过有限个CP脉冲后都能进入有效状态环,则称它是可自启动的。
设计方法
- 逻辑抽象,得出电路的状态转换图或状态转换表
- 状态化简。如果两个电路状态在相同的输入下有相同的输出,并且转换到同一个次态中,则为等价。可以合并为一个。
- 状态分配
- 选定触发器,求出状态方程、驱动方程、输出方程
- 画出逻辑图
- 检查能否自启动
常用的时序逻辑电路
移位寄存器
同步计数器
PT是计数允许端,CP是时钟信号。Cr是异步清零,ABCD是在LD有效时的置数输入。Oc是进位端。
任意进制计数器的构成方法
已有N进制计数器,需要M进制计数器
M< N时
- 置零法
- 置数法
M>N时
将多片N进制计数器组合起来,构成M进制计数器。可以分为串行进位方式、并行进位方式、整体置零方式。