基础知识
多项式求值
对于形如下式的多项式
\[P(x)=2x^4+3x^3-3x^2+5x-1 \]
如果我们普通地代入计算,则会需要计算10次乘法,以及4次加法。这显然不是最优的,更优的方法例如秦九韶算法,将多项式重写为
\[P(x)=-1+x*(5+x*(-3+x*(3+x*2))) \]
此时再代入值计算,则只用4次乘法和4次加法。一般来说\(d\)阶多项式可以通过\(d\)次乘法和\(d\)次加法求值。
标准形式的多项式
\[P(x) = c_1+c_2x+c_3x^2+c_4x^3+c_5x^4 \]
可以写成
\[P(x)=c_1+x(c_2+x(c_3+x(c_4+x(c_5)))) \]
或者也有更一般的形式,可以用于之后的插值计算
\[P(x)=c_1+(x-r_1)(c_2+(x-r_2)(c_3+(x-r_3)(c_4+(x-r_4)(c_5)))) \]
其中称\(r1,r2,r3,r4\)为基点。
二进制数字
二进制数字可以表示为:
\[\cdots b_2b_1b_0b_{-1}b_{-2}\cdots \]
其等价于十进制下的
\[\cdots b_22^2+b_12^1+b_02^0+b_{-1}2^{-1}+b_{-2}2^{-2}\cdots \]
十进制转化为二进制
例如\(53.7\)转化为二进制,可以拆分为整数部分和小数部分,分别转化,然后在拼接起来。
整数部分
将整数连续除以\(2\),记录余数,直到整数最后变为\(0\),余数反过来排列在一起就是二进制表示。例如
\[53\div 2 = 26\cdots1 \]
\[26\div 2 = 13\cdots0 \]
\[13\div 2 = 6\cdots1 \]
\[6\div 2 = 3\cdots0 \]
\[3\div 2 = 1\cdots1 \]
\[1\div 2 = 0\cdots1 \]
那么二进制表示就是\(110101\)
小数部分
将小数部分不断乘以\(2\),得到的结果保留整数部分,直到小数部分为\(0\),整数部分顺序排列即为小数部分的二进制表示
例如
\[0.7*2 = 0.4+1 \]
\[0.4*2 = 0.8+0 \]
\[0.8*2 = 0.6+1 \]
\[0.6*2 = 0.2+1 \]
\[0.2*2 = 0.4+0 \]
\[0.4*2 = 0.8+0 \]
\[\vdots \]
后面重复,代表在二进制中是无限循环小数。有\((0.7)_{10}=(0.1\overline{0110})_2\)
最后有\((53.7)_{10} = (110101.1\overline{0110})_2\)。
二进制转化为十进制
开头已经介绍过一般情况,对于有限小数是容易计算的。
无限小数时,例如\(x=(0.\overline{1011})_2\),先左移\(4\)位,再减去原始的\(x\),有
\[2^4x = 1011.\overline{1011}\\ x=0000.\overline{1011} \]
相减得
\[(2^4-1)x = (1101)_2 = (11)_{10} \]
求解\(x\)可得,\(x=(0.\overline{1011})_2=11/15\)。
实数的浮点表示
本节按照IEEE754标准。
浮点格式
一个浮点数字包含三个部分:符号(正负)、尾数(包含一串有效数位)和一个指数,这些部分都在一个计算机字(WORD)里。
浮点数常用三种精度级别:单精度、双精度、扩展精度。它们分配的数位分别是32、64、80。具体如下
| 精度 | 符号 | 指数 | 尾数 |
|---|---|---|---|
| 单精度 | 1 | 8 | 23 |
| 双精度 | 1 | 11 | 52 |
| 扩展精度 | 1 | 15 | 64 |
三种精度以相同的方式运行。标准化的IEEE浮点数表示为
\[\pm 1.bbb\cdots b\times 2^p \]
其中\(N\)个\(b\)或0或1,\(p\)是一个\(M\)位的二进制数表示指数。最左边的一位(主导数位)必须是\(1\)。
当一个二进制数用一个标准浮点数字表示的时候,它被称为“左对齐”,意味着其中最左边的一个数位\(1\)被平移到小数点的左边,平移通过指数的变化来补偿,例如,十进制数\(9\),对应的二进制数\(1001\)保存为
\[+1.001\times 2^3 \]
以双精度(\(M=11,N=52\))为例,1的双精度表示为
\[+1.0000000000000000000000000000000000000000000000000000\times 2^0 \]
其中有52位尾数,下一个比\(1\)大的浮点数是
\[+1.0000000000000000000000000000000000000000000000000001\times 2^0 \]
或者说是\(1+2^{-52}\)
定义1
机器精度对应的数字,记作\(\varepsilon_{math}\),是\(1\)和比\(1\)大的最小浮点数之间的距离。对于双精度来说就是\(2^{-52}\)
如果一个小数是无限小数,或者是超过了52位的小数,IEEE规定,如果在第53位为0,则52位以后的全部社区,如果53位为1,则在52位上加1。特别的,如果第53位为1,其后所有已知位为0,那么当且仅当52位是1时在52位上加1。
上述方法称为IEEE舍入最近法则。
定义2
将IEEE双精度浮点数字记做\(x\),利用舍入最近法则记做\(fl(x)\)
在计算机算术中,实数\(x\)用一串数位\(fl(x)\)替换。根据这个定义,\(9.4\)在二进制中表示如下
\[+1.0010110011001100110011001100110011001100110011001100|110\cdots\times 2^3 \]
则\(fl(9.4)\)表示为
\[+1.0010110011001100110011001100110011001100110011001101\cdots\times 2^3 \]
我们通过去掉最右边无穷长的数字尾巴\(0.\overline{1100}\times 2^{-52}\times 2^3=\overline{0.0110}\times 2^{-51}\times 2^3=0.4\times 2^{-48}\)得到浮点表达。并在舍入过程中加上\(2^{-52}\times 2^3=2^{-49}\)。因而
\[fl(9.4) = 9.4+2^{-49}-0.4\times 2^{-48}\\ =9.4+(1-0.8)2^{-49}\\ =9.4+0.2\times 2^{-49} \]
换句话说,将\(9.4\)保存为双精度浮点数时可能产生了\(0.2\times 2^{-49}\)的误差,我们把它称作舍入误差。
定义3
令\(x_c\)是计算版本\(x\)的精确度量,则
\[绝对误差=|x_c-x| \]
\[相对误差=\frac{|x_c-x|}{|x|}(x\neq 0) \]
相对舍入误差
在IEEE机器算术模型中,\(fl(x)\)的相对舍入误差不会比机器精度的一半大:
\[\frac{|fl(x)-x|}{|x|}\leq \frac{1}{2}\varepsilon_{math} \]
浮点数的机器表示
每个双精度浮点数字被分配了8字节,或者说64位,来存储对应的三个部分。每个字都有如下形式
\[se_1e_2\cdots e_{11}b_1b_2\cdots b_{52} \]
其中第1位保存了符号位,后面11位用于保存指数,再后面小数点后的52位保存尾数。符号位0是正数,1是负数。11位指数表示的正二进制整数,这些正数通过往指数上叠加\(2^10-1=1023\)得到,指数范围在\(-1022\)和\(1023\)之间,\(e_1\cdots e_{11}\)覆盖了从\(1\)到\(2046\)之间对应的指数,由于特殊目的,没有使用\(0\)和\(2047\)。
数字\(1023\)称为双精度格式的指数偏差。它被用于把正和负指数转化为正的二进制数保存在指数位中,对于单精度和扩展精度,指数偏差位分别是127和16383.
也就是说,指数位上的数字,减去1023才是浮点数中所应该是的指数。
再来看特殊值\(2047\)。如果尾数位串都是0,则用于表示\(\infty\)(其符号取决于第一位),否则表示\(NaN\),意为不是一个数字。
例如\(1/0\)是\(+\inf\),前\(12\)位用十六进制表示为7FF,后面全是0.
\(-1/0\)是\(-\inf\),前\(12\)位用十六进制表示为FFF,后面全是0.
\(0/0\)是\(NaN\),前\(12\)位用十六进制表示为FFF,后面不全是0.
再来看特殊值\(0\),意味着\(e_1e_2\cdots e_{11}=(000 0000 0000)_2\)。其表示一个非标准浮点数
\[\pm 0.b_1b_2\cdots b_{52}\times 2^{-1022} \]
由上可见,第一位不再假设为1.这样的非标准化数字称作异常浮点数字。这样就扩展了数字的表示范围,因而,最小的可表达的双精度数字是\(2^{-52}\times 2^{-1022}\)。
另外\(+0,-0\)也是一个异常数字。计算中它们被看作是相同的两个实数。
浮点数加法
首先对齐进行加法的两个数字的小数点位,接着相加,然后把结果保存为浮点数字。
在加法寄存器中,可以进行超过52位的加法,但是在相加之后必须舍入变回52位。
有效数字缺失
有一个主要问题以多种形式出现,该问题是由于对近似相等的两个数字相减造成有效数字的位数减少。
例如\(123.4567-123.4566=0.0001\),有效数字从原来的七位减少到一位。
很多情况下我们可以通过重新构造计算来解决这个问题。
例1
在三位小数的计算机上计算\(\sqrt{9.01}-3\)
正确的结果接近\(1.6662\times 10^{-3}\),但当我们使用三位有效数字时,由于\(\sqrt{9.01}\approx 3.0016662\),保存三位有效数字时得到\(3.00\)。再减去\(3.00\),得到\(0.00\),没有一个有效数位是正确的。
但是我们可以用以下方法挽救
\[\sqrt{9.01}-3 = \frac{(\sqrt{9.01}-3)(\sqrt{9.01}+3)}{\sqrt{9.01}+3}=\frac{9.01-9}{\sqrt{9.01}+3} \]
\[=\frac{0.01}{3.00+3.00}=\frac{0.01}{6}=0.00167\approx 1.67\times 10^{-3} \]
这种方法本质上是一个窍门。称作“共轭等式”。通常会使用一些特定的恒等式,例如三角恒等式。
例如
\[E_1=\frac{1-cosx}{sin^2x},E_2=\frac{1}{1+cosx} \]
两个式子虽然等价,但是在数值计算上,输入一个较为靠近0的数,则第二个比第一个精度高。
例2
解方程\(ax^2+bx+c=0\)
对于最基础的求根公式
\[x=\frac{-b\pm \sqrt{b^2-4ac}}{2a} \]
其中间取负号问题可能不大,但是取正号时,如果\(ac\)相对于\(b^2\)非常小,则分式上面会直接舍入等于0,造成整个结果等于0.
为了解决这个问题,可以在\(b\)是正数时
\[x_1=-\frac{b+\sqrt{b^2-4ac}}{2a},x_1=-\frac{2c}{b+\sqrt{b^2-4ac}} \]
\(b\)是负数时
\[x_1=\frac{-b+\sqrt{b^2-4ac}}{2a},x_1=\frac{2c}{-b+\sqrt{b^2-4ac}} \]
微积分回顾
书中回顾了函数的连续性、罗尔定理、拉格朗日中值定理、泰勒展开、积分中值定理等。
求解方程
二分法
方法
定义1
如果\(f(r)=0\),函数\(f(x)\)在\(x=r\)时有一个根。
定理1
根据函数的连续性,我们知道,如果一个函数是连续的(在[a,b]上),并且在\(a< b\)时有\(f(a)f(b)<0\),那么函数在\((a,b)\)之间至少有一个根\(r\)使得\(f(r)=0\)
显然,我们可以判断\(c=(b+a)/2\)时\(f(a)f(c)\)的符号来判断根具体在\([a,c]\)还是\([c,b]\)之中
由此我们就可以得到一个求出根的伪代码
二分法
给定初始区间[a,b]使得f(a)f(b)<0
while (b-a)/2>TOL
c = (a+b)/2
if f(c)=0,stop,end
if f(a)f(c)<0
b = c
else
a = c
end
end
最终的区间[a,b]中包含一个根
近似根为(a+b)/2
显然我们求出的是一个区间\([a,b]\),有一个根在其中,我们只能估计一个值。另外代码中的TOL指的是精度,即这个根在\((a+b)/2\pm TOL\)这个范围内。
分析
现在来分析二分法的精确度和收敛速度。
假设\([a,b]\)是初始区间,在\(n\)次二分之后,得到的最终区间\([a_n,b_n]\)的长度为\((b-a)/2^n\)。选择中点\(x_c=(a_n+b_n)/2\)为解的最优估计值,与真实值的误差不会超过区间长度的一般。总之,n步二分法之后,我们得到
\[求解误差=|x_c-r|<\frac{b-a}{2^{n+1}} \]
\[函数计算次数=n+2 \]
对于其精度,每一次函数计算后,解的不确定性都会减少一半。
定义2
如果误差小于\(0.5\times 10^{-p}\),解精确到小数点后\(p\)位。
不动点迭代
举一个例子,以弧度制计算\(\cos\)。以任意值代入,比如我们代入\(1\).有\(cos1=0.5403\cdots\),再将结果代入,有\(cos(cos1)=0.85755\cdots\),以此类推,多次代入后,我们发现无论初始值是多少,最后都会收敛到\(0.7390851332\cdots\)
函数的不动点
定义1
当\(g(r)=r\),实数\(r\)是函数\(g\)的不动点。
例如,我们求解\(\cos x-x=0\)的方程,用不动点的视角来看,就是求解\(\cos x=x\),或者说求解\(\cos x\)的不动点。
一旦方程写做\(g(x)=x\),从一个初始估计\(x_0\)开始进行不动点迭代过程,对函数\(g\)进行迭代,
\[x_1=g(x_0)\\ x_2=g(x_1)\\ x_3=g(x_2)\\ \vdots \]
依此下去。当进行无穷多步迭代后序列\(x_i\)可能收敛,也可能不收敛。但是,如果函数\(g\)是一个连续函数并且\(x_i\)收敛,收敛到一个数字\(r\),那么\(r\)就是对应的不动点。意味着
\[g(r) = g(\lim_{i\to\infty}x_i)=\lim_{i\to\infty}g(x_i) = \lim_{i\to\infty}x_{i+1}=r \]
所有方程\(f(x)=0\)都能转化为\(g(x)=x\)来不动点迭代吗?答案是肯定的。
虽然都能迭代,但不总是能收敛的。
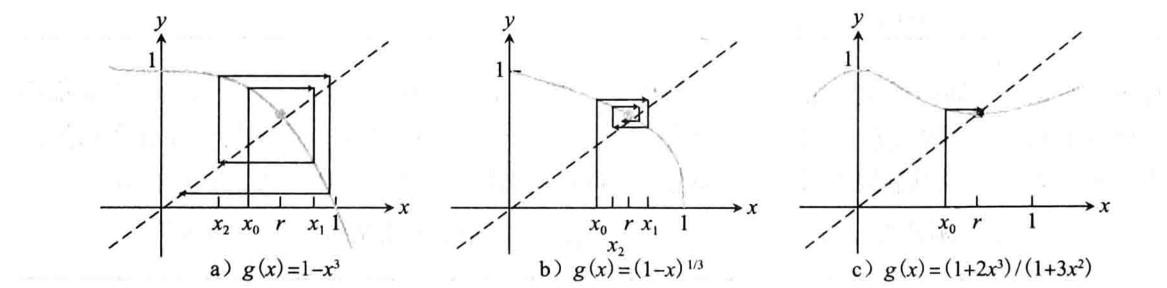
例如\(x^3+x-1=0\)换成\(x=1-x^3\)来迭代,最后结果就会在\(1,0\)之间摆动,这是因为\(g(0)=1,g(1)=0\)。
但是,如果使用\(x=\sqrt[3]{1-x}\)来迭代,就可以求出正确的不动点\(x=0.6823\cdots\)。迭代了大概25次。
如果使用\(x=(1+2x^3)/(1+3x^2)\),也可以收敛,并且只需要迭代4次就可以得到\(x=0.6823\cdots\)。
不动点迭代几何
我们要解释出现上述差异的原因。
如下图,将\(g(x),x\)画在同一坐标系下,其中交点就是不动点,图中的箭头代表迭代过程。这种表示又被称作cobweb图。
图\(a\)中迭代逐渐远离了不动点,而\(b,c\)两图,迭代都在不断靠近不动点。
由图我们猜测迭代收敛与否和\(g(x)\)在不动点附近的斜率有关。
不动点迭代的线性收敛
以\(g_1(x)=-\frac{3}{2}x+\frac{5}{2},g_2(x)=-\frac{1}{2}x+\frac{3}{2}\)为例。它们的不动点都是\(x=1\)。
我们把\(g(x)\)写作\(x-r\)的形式,其中\(r=1\):
\[g_1(x)=-\frac{3}{2}(x-1)+1\\ g_1(x)-1=-\frac{3}{2}(x-1)\\ x_{i+1}-1=-\frac{3}{2}(x_i-1) \]
如果我们把\(e_i=|r-x_i|\)作为第\(i\)步时的误差,可以看到上式的误差是\(e_{i+1}=3e_i/2\),意味着误差越来越大,也就是发散。
对于\(g_2(x)\)有
\[x_{i+1}-1=-\frac{1}{2}(x_i-1) \]
\(e_{i+1}=e_i/2\),误差越来越小,就是收敛。
定义2
令\(e_i\)表示迭代过程中第\(i\)步时的误差,如果
\[\lim_{i\to\infty}\frac{e_{i+1}}{e_i}=S<1 \]
该方法被称为满足线性收敛,收敛速度为\(S\)。
这样的推理过程也可以适用于更加一般的连续可微函数
定理1
假设函数\(g\)是连续可微函数,\(g(r)=r,S=|g'(r)|<1\),则不动点迭代对于一个足够接近\(r\)的初始估计,以速度\(S\)线性收敛到不动点\(r\)。
定义3
如果迭代方法对于一个足够接近\(r\)的初值能收敛到\(r\),该迭代方法称为局部收敛到\(r\)。
终止条件
同二分法不同,FPI没有误差与迭代次数的关系公式,必须决定何时终止算法,这称为终止条件。
对于一组容差\(TOL\),我们可能使用绝对终止条件
\[|x_{i+1}-x_i| < \text{TOL} \]
当解不在\(0\)附件时可以使用相对误差条件
\[\frac{|x_{i+1}-x_i|}{|x_{i+1}|} < \text{TOL} \]
还有混合绝对/相对误差终止条件
\[\frac{|x_{i+1}-x_i|}{max(|x_{i+1}|,\theta)} < \text{TOL} \]
其中\(\theta>0\),常常用于\(0\)附近的解。此外,如果收敛失败,一个好的FPI也应该设置迭代次数上限。
二分法可以保证线性收敛,不动点迭代仅仅是局部收敛。不动点迭代收敛时,是线性收敛。二分法每次可以去掉\(1/2\)的不确定性,而FPI的不确定性每次会乘上\(S=|g'(r)|\),因此可能比二分法更快或更慢,依赖于\(S\)比\(1/2\)更大还是更小。
精度的极限
前向与后向误差
定义1
假设\(f\)是一个函数,\(r\)是一个根,意味着满足\(f(r)=0\)。假设\(x_a\)是\(r\)的近似值。对于根求解问题,近似\(x_a\)的后向误差是\(|f(x_a)|\),前向误差是\(|r-x_a|\)。
举个例子,求解以下函数的根
\[f(x) = x^3-2x^2+\frac{4}{3}x-\frac{8}{27} \]
我们可以通过手算验证\(2/3\)是它的根。
当我们使用双精度浮点数去二分法求解时,最后可能解出\(r=0.6666641\),并且到此结束,因为此时\(f(r)=0\),意味着其等于机器\(0\)。在这\(2/3\pm 10^{-5}\)的范围上,其函数值都等于机器\(0\)。
事实上,\(r\)的后向误差接近\(\varepsilon_{math}=2.2\times 10^{-16}\),而前向误差在大约\(10^{-5}\)。双精度不能在机器精度的相对误差下可靠计算,从而导致了一个范围内的数最终都等于机器\(0\)。
事实上\(2/3\)是这个函数的三重根
定义2
假设\(r\)是可微函数\(f\)的根,如果\(0=f(r)=f'(r)=f''(r)=\cdots=f^{(m-1)}(r)\),但是\(f^{(m)}(r)\neq 0\),就说\(f\)在\(r\)点具有\(m\)重根。多于一个根的叫重根,只有一个根的叫单根。
由于函数在多根附近十分平缓,前向和后向误差之间在近似解的附近存在很大的不一致。后向误差在垂直方向进行度量,通常比在水平方向度量的前向误差小得多。
前向和后向误差的讨论和方程求解器的终止条件有关。我们有两种方法更加接近方程的根
- 使得\(|x_a-r|\)足够小
- 使得\(|f(x_a)|\)足够小
具体选择使用哪一种,取决于问题所处的环境。对于二分法,两种误差都可以观察到。而FPI只能知道后向误差,而不可能知道前向误差。
威尔金森多项式
一个难以进行数值求解的单根例子在威尔金森的论著中进行了讨论,威尔金森多项式是
\[W(x) = (x-1)(x-2)\cdots(x-20) \]
但当我们把它展开,并用二分法等方法却很难求出正确的解,精确度甚至不到第二个小数。
这主要是因为其展开式的每一项的常数太大,例如常数项是\(2432902008176640000\),这导致在求值计算中会由于近似相等、大数字的消去而有损失。
但是若不展开,代入求根器中却能算出精确根。当然如果已经分解好了,也就没有求解的必要了。
根搜索的敏感性
威尔金森多项式和多重根的问题,其本质都是方程中小的求解误差造成求解根中的大误差。
如果在输入中是一个小误差,在这种情况下对问题进行求解,造成输出中的大问题,这样的问题被称作敏感性问题。
假设问题是找到\(f(x)=0\)的根\(r\),但是对输入做了一个小变化\(\varepsilon g(x)\),其中\(\varepsilon\)很小。令\(\Delta r\)是对应根中的变化,因而
\[f(r+\Delta r)+\varepsilon g(r+\Delta r)=0 \]
将\(f\)和\(g\)一阶泰勒展开,有
\[f(r)+(\Delta r)f'(r)+\varepsilon g(r)+\varepsilon(\Delta r)g'(r)+O((\Delta r)^2) \]
对于小的\(\Delta r\),直接忽略掉\(O((\Delta r)^2)\),有
\[(\Delta r)(f'(r)+\varepsilon g'(r))\approx-f(r)-\varepsilon g(r)=-\varepsilon g(r) \]
假设和\(f'(r)\)相比,\(\varepsilon\)很小,则又有
\[\Delta r\approx\frac{-\varepsilon g(r)}{f'(r)+\varepsilon g'(r)}\approx -\varepsilon\frac{g(r)}{f'(r)} \]
上式就叫做根的敏感公式。(假设\(r\)是\(f(x)\)的根,并且\(r+\Delta r\)是\(f(x)+\varepsilon g(x)\)的根,则当\(\varepsilon << f'(r)\)时有上式)
对于一个一般算法生成的近似\(x_c\),我们定义
\[误差放大因子=\frac{相对前向误差}{相对后向误差} \]
条件
条件数也是误差放大度量的一种方式。数值分析是对算法的研究,算法把定义问题的数据作为输入,对应的结果作为输出。条件数指的是理论问题本身所带来的的误差放大部分,和用于求解问题的特定算法无关。
问题的条件数定义为所有输入变化,或者至少规定类型的变化所造成的最大误差放大。
条件数高的问题称为病态问题,条件数在\(1\)附件的问题称为良态问题。
牛顿方法
为了找到\(f(x)=0\)的根,给定一个初始估计\(x_0\),画出函数\(f\)在\(x_0\)的切线。用切线来近似函数\(f\),求出其与\(x\)轴的交点作为\(f\)的根。由于函数\(f\)的弯曲,该交点可能不是精确解,因而该步骤要迭代进行。
\[x_0=初始估计 \]
\[x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)},\quad i=0,1,2,\cdots \]
牛顿方法的二次收敛
定义1
令\(e_i\)表示一个迭代方法第\(i\)步后得到的误差。该迭代是二次收敛,如果满足下式
\[M=\lim_{i\to\infty}\frac{e_{i+1}}{e^2_i}<\infty \]
定理1
令\(f\)是二阶连续可微函数,\(f(r)=0\)。如果\(f'(r)\neq 0\),则牛顿方法局部二次收敛到\(r\)。第\(i\)步的误差\(e_i\)满足
\[\lim_{i\to\infty}\frac{e_i}{e_i^2}=M \]
其中
\[M=\frac{f''(r)}{2f'(r)} \]
也可被看作
\[e_{i+1}\approx M e_i^2 \]
对于线性收敛方法,这个误差公式应该和\(e_{i+1}\approx Se_i\)进行比较,FPI方法中\(S=|g'(r)|\),二分法中\(S=1/2\)
尽管\(S\)对线性收敛很关键,但是\(M\)的值并不是很重要,这是由于其包含了平方,只要\(M\)不太大,误差就会进一步下降。
牛顿方法的线性收敛
上面的定理并不意味着牛顿方法总能二次收敛。
例如求\(f(x)=x^2\)的实根,牛顿法如下
\[x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)}=\frac{x_i}{2} \]
仅仅每步除以\(2\).对于其他幂函数也有类似的结果。
定理1
假设在区间\([a,b]\)上,\((m+1)\)阶连续可微函数\(f\)在\(r\)点有一个\(m\)阶多重根,则牛顿方法局部收敛到\(r\),第\(i\)步误差\(e_i\)满足
\[\lim_{i\to \infty}\frac{e_{i+1}}{e_i}=S \]
其中\(S=(m-1)/m\)
事实上,牛顿法在单根位置上,\(f'(r)\neq 0\),具有二次收敛速度,在多根位置上\(f'(r)=0\),收敛式线性的。
定理2
如果在\([a,b]\)区间上\(f\)是\((m+1)\)阶连续函数,包含\(m>1\)的多重根,则改进的牛顿方法
\[x_{i+1}=x_i-\frac{mf(x_i)}{f'(x_i)} \]
收敛到\(r\),并具有二次收敛速度。
牛顿法如同FPI,也可能不会收敛到根。例如两个数循环出现、某一步\(f'(x_i)=0\)等。
不需要导数的根求解
虽然牛顿法在非重根时表现的比二分法和FPI更好,因为它获取了“导数”这个额外信息。但有时候我们可能难以计算导数。
这种情况下,割线方法就是一个好的替代。它使用近似值割线替代了切线,并且收敛速度差不多快。
割线方法及其变体
不难想到,直接用差商
\[\frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} \]
去近似替换牛顿法中的\(f'(x_i)\),就得到了割线方法
\[x_0,x_1=初始估计 \]
\[x_{i+1}=x_i-\frac{f(x_i)(x_i-x_{i-1})}{f(x_i)-f(x_{i-1})},i=1,2,3,\cdots \]
假设割线方法收敛到函数\(f\)的根\(r\),且\(f'(r)\neq 0\),近似误差关系
\[e_{i+1}\approx \bigg|\frac{f''(r)}{2f'(r)}\bigg|e_ie_{i-1} \]
成立并且
\[e_{i+1}\approx \bigg|\frac{f''(r)}{2f'(r)}\bigg|^{\alpha-1}e_i^\alpha \]
其中\(\alpha = (1+\sqrt 5)/2\approx 1.62\)。割线方法以超线性的速度收敛到一个单根,意味着它在线性和二次收敛方法之间。
割线方法有三种推广形式,它们也很重要。
试位方法(Regula Falsi)
和二分法相似,但是其中的中点被类似割线方法的近似所替换,给定区间\([a,b]\),该区间包含根(假设\(f(a)f(b)<0\)),使用割线方法定义下一个点为
\[c = a-\frac{f(a)(a-b)}{f(a)-f(b)}=\frac{bf(a)-af(b)}{f(a)-f(b)} \]
根据\(f(a)f(c)<0\)或者\(f(c)f(b)<0\),分别选择新的区间\([a,c]\)或\([c,b]\),新的区间仍然可以括住根。
通常试位方法会表现地比二分法和割线方法都好,但是试位方法不能包子每一步都消除一半的不确定性,有时收敛会很慢。
Muller方法
该方法不是计算经过先前两个点的直线和\(x\)轴的交点,而是使用桑耳前面生成的点\(x_0,x_1,x_2\),画出通过它们的抛物线\(y=p(x)\),并计算抛物线和\(x\)轴的交点。
书上并没有详细介绍这个方法。
逆二次插值(IQI)
是割线方法到抛物线的一种相近的泛化方法。但是使用形如\(x=p(y)\)的抛物线,而不是Muller方法中的\(y=p(x)\)。
我们的问题可以立刻求解:这个抛物线和\(x\)轴只有一个交点,所以从上一步中的三个估计\(x_i,x_{i+1},x_{i+2}\)寻找\(x_{i+3}\),这个过程中没有混淆。
经过三点\((a,A),(b,B),(c,C)\)的二阶多项式\(x=P(y)\)为
\[P(y) = a\frac{(y-B)(y-C)}{(A-B)(A-C)}+b\frac{(y-A)(y-C)}{(B-A)(B-C)}+c\frac{(y-A)(y-B)}{(C-A)(C-B)} \]
这是一个拉格朗日插值的例子,用\(y=0\)代入,得到和\(x\)轴的交点,经过重新组合与替代,我们得到
\[P(0)=c-\frac{r(r-q)(c-b)+(1-r)s(c-a)}{(q-1)(r-1)(s-1)} \]
其中\(q=f(a)/f(b),r=f(c)/f(b),s=f(c)/f(a)\)
对于IQI,设置
\[a=x_i,b=x_{i+1},c=x_{i+2},A=f(x_i),B=f(x_{i+1}),C=f(x_{i+2}) \]
下一步的估计\(x_{i+3}=P(0)\)为
\[x_{i+3}=x_{i+2}-\frac{r(r-q)(x_{i+2}-x_{i+1})+(1-r)s(x_{i+2}-x_{i})}{(q-1)(r-1)(s-1)} \]
其中\(q=f(x_{i})/f(x_{i+1}),r=f(x_{i+2})/f(x_{i+1}),s=f(x_{i+2})/f(x_{i})\)
Brent方法
这是一种混合方法,该方法使用前面介绍的迭代技术,推出一个新的方法。
该方法用于连续函数\(f\),区间的边界是\(a\)和\(b\),同时\(f(a)f(b)<0\)。Brent方法记录当前点\(x_i\),该点具有最优的后向误差,同时有包含根的区间\([a_i,b_i]\)。简单来讲,尝试使用逆二次方法,并在下述情况下,使用结果来替代\(x_i,a_i,b_i\)中的一个
- 后向误差得到改进
- 包含根的区间至少减小一半
否则,尝试使用割线方法以实现相同的目的,如果割线方法也失败了,则使用二分法,保证至少减少一半的不确定性。
方程组
高斯消元法
朴素的高斯消元法
和线性代数中介绍的一致
对于一个线性方程组可以进行三种操作
- 两个方程彼此交换位置
- 在一个方程上加上或减去另外一个方程的倍数
- 对于一个方程乘以非零的常数
通常我们也会使用增广矩阵来替代方程组。
操作次数
引理1
对于任何正整数\(n\)
- \(1+2+3+\cdots+n = n*(n+1)/2\)
- \(1^2+2^2+\cdots+n^2 = n(n+1)(2n+1)/6\)
消去某一列在主对角线下的元素,以第一列为例,将第二行变为如下形式
\[\begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} & | & b_1\\ 0 & a_{22}-\frac{a_{21}}{a_{11}}a_{12} & \cdots & a_{2n}-\frac{a_{21}}{a_{11}}a_{1n} & | &b_2-\frac{a_{21}}{a_{11}}b_1 \end{matrix} \]
其他行同理,其中\(a_{11}\)在操作中作为除数,这样的数字称为主元。不难得知,如果主元为\(0\),算法会终止,这是朴素办法的一个问题。
高斯消元法中消去步骤的操作次数
\(n\)个方程\(n\)个未知数的消去计算(下三角除了对角线的部分转换为\(0\)),可以在\(2n^3/3+n^2/2-7n/6\)次操作后完成
消去之后,矩阵变成上三角形式,之后从最后一个未知数往回带进行求解。
高斯消元法中回代过程的操作次数
\(n\)个方程\(n\)个未知数的三角形系统的回代过程,可以在\(n^2\)次操作后完成
综上,消去的事件复杂度为\(O(n^3)\),回代是\(O(n^2)\),总的是\(O(n^3)\)
LU分解
高斯消元法的矩阵形式
继续同线性代数,我们可以把方程组写成一个矩阵和一个向量相乘的形式,即\(\bm A\bm x=\bm b\)
吧方程组写成矩阵的形式的优势在于可以使用矩阵运算。LU分解是高斯消元法的矩阵形式。它包含把系数矩阵\(A\)写做下三角矩阵\(L\)和上三角矩阵\(U\)的乘积
我们有关于LU分解的三个事实
- 令\(L_{ij}(-c)\)表示下三角矩阵,其主对角线上的元素为\(1\),在\((i,j)\)位置上的元素为\(-c\)。则\(A\to L_{ij}(-c)A\)表示行运算“从第\(i\)行中减去第\(j\)行的\(c\)倍”。
例如\(L_{21}(-c)\)
\[A= \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{bmatrix}\to \begin{bmatrix} 1 & 0 & 0\\ -c & 1 & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{bmatrix} \]
\[=\begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21}-ca_{11} & a_{22}-ca_{12} & a_{23}-ca_{13}\\ a_{31} & a_{32} & a_{33} \end{bmatrix} \]
- \(L_{ij}(-c)^{-1}=L_{ij}(c)\)
- 下面的矩阵乘积成立
\[\begin{bmatrix} 1 & & 0\\ c_1 & 1 & \\ & & 1 \end{bmatrix} \begin{bmatrix} 1 & & \\ & 1 & \\ c_2 & & 1 \end{bmatrix} \begin{bmatrix} 1 & & \\ & 1 & \\ & c_3 & 1 \end{bmatrix} \begin{bmatrix} 1 & & \\ c_1 & 1 & \\ c_2 & c_3 & 1 \end{bmatrix} \]
根据以上事实,我们可以把系数矩阵\(A\)表示为\(A=LU\),其中\(U\)和高斯消元得到的上三角矩阵相同,而\(L\)矩阵就是所进行的操作乘起来的矩阵。
使用LU分解回代
一旦知道\(L,U\),问题\(Ax=b\)就可以转化为\(LUx=b\)。定义\(c=Ux\),则回代有两个步骤
- 对于方程\(Lc=b\),求解\(c\)
- 对于方程\(Ux=c\),求解\(x\)
其中\(Lc=b\)因为\(L\)是下三角矩阵,从上往下回代,\(Ux=c\)因为\(U\)是上三角矩阵,从下往上回代。
LU分解的复杂度
如果只有一个方程组,那么和高斯消元法没有区别
但是,如果我们遇到的问题是
\[Ax=b_1\\ Ax=b_2\\ \cdots\\ Ax=b_k \]
这样的。那LU分解会比高斯消元一个一个去计算要来得快。
但是,并不是所有的矩阵都可以进行\(LU\)分解
例如分解
\[\begin{bmatrix} 0 & 1\\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0\\ a & 1 \end{bmatrix} \begin{bmatrix} b & c\\ 0 & d \end{bmatrix}= \begin{bmatrix} b & c\\ ab & ac+d \end{bmatrix} \]
由于\(ab=1,b=0\)不可能同时成立,所以反证法得知不能分解。
误差来源
误差放大和条件数
定义1
向量\(x=(x_1,\cdots,x_n)\)的无穷范数或者最大范数为\(||x||_\infty=max|x_i|\),即\(x\)所有元素中的最大绝对值。
定义2
令\(x_a\)是线性方程组\(Ax=b\)的近似解。余项是向量\(r=b-Ax_a\),后向误差是余项的范数\(||b-Ax_a||_\infty\),前向误差是\(||x-x_a||_\infty\)
同时也定义相对后向误差为
\[\frac{||r||_\infty}{||b||_\infty} \]
相对前向误差定义为
\[\frac{||x-x_a||_\infty}{||x||_\infty} \]
这个方程的误差放大因子是二者的比率,即
\[误差放大因子=\frac{相对前向误差}{相对后向误差} \]
定义3
方阵\(A\)的条件数\(cond(A)\)为求解\(Ax=b\)时,对于所有右侧向量\(b\),可能出现的最大误差放大因子。
和向量范数类似,定义\(n\times n\)矩阵\(A\)的矩阵(无穷)范数为
\[||A||_\infty = 每行元素绝对值之和的最大值 \]
定理1
\(n\times n\)矩阵\(A\)的条件数是
\[cond(A) = ||A||\cdot||A^{-1}|| \]
依据误差放大因子,在求解\(Ax=b\)可能出现的相关前向误差是\(\varepsilon_{math}\cdot cond(A)\)。换句话说,如果\(cond(A)\approx 10^k\),我们在计算\(x\)时,将丢掉\(k\)位数字精度。
向量范数和矩阵范数的性质
对于向量无穷范数
- \(||x||\geq 0\),当且仅当\(x=[0,\cdots,0]\)时等号成立
- 对于每个标量\(\alpha\)和向量\(x\),\(||\alpha x||=|\alpha|\cdot ||x||\)
- 对于向量\(x,y\)有\(||x+y||\leq||x||+||y||\)
对于矩阵无穷范数
- \(||A||\geq 0\),当且仅当\(A=0\)时等号成立
- 对于每个标量\(\alpha\)和向量\(x\),\(||\alpha A||=|\alpha|\cdot ||A||\)
- 对于矩阵\(A,B\)有\(||A+B||\leq||A||+||B||\)
被称为算子范数的矩阵范数,也可以使用特定的向量范数进行定义
\[||A||=\max \frac{||Ax||}{||x||} \]
对于任意矩阵\(A\)和向量\(x\)满足
\[||Ax||\leq ||A||\cdot||x|| \]
淹没
考虑如下方程组
\[10^{-20}x_1+x_2=1\\ x_1+2x_2=4 \]
高斯消元如下
\[\begin{bmatrix} 10^{-20} & 1 & | & 1\\ 1 & 2 & | & 4 \end{bmatrix}\to \begin{bmatrix} 10^{-20} & 1 & | & 1\\ 0 & 2-10^{20} & | & 4-10^{20} \end{bmatrix} \]
然后解出
\[[x_1,x_2]=\bigg [\frac{2\times 10^{20}}{10^{20}-2},\frac{4-10^{20}}{2-10^{20}}\bigg]\approx[2,1] \]
我们手算是可以这样的,但是当我们使用IEEE双精度的时候,
\[\begin{bmatrix} 10^{-20} & 1 & | & 1\\ 0 & 2-10^{20} & | & 4-10^{20} \end{bmatrix} \]
舍入得
\[\begin{bmatrix} 10^{-20} & 1 & | & 1\\ 0 & -10^{20} & | & -10^{20} \end{bmatrix} \]
然后首先解出\(x_2=1\),然后\(x_1=0\),与精确解相比相差巨大。
我们的解决办法是,更换行顺序,
\[\begin{bmatrix} 1 & 2 & | & 4\\ 10^{-20} & 1 & | & 1 \end{bmatrix}\to \begin{bmatrix} 1 & 2 & | & 4\\ 0 & 1-2\times 10^{-20} & | & 1-4\times 10^{-20} \end{bmatrix} \]
舍入后也可以得到\(x_2=1\),然后\(x_1=2\)。
上述例子告诉我们,高斯消去的过程中要尽可能保证乘子比较小。
PA=LU分解
部分主元
部分主元要求,在每一次选择主元时,找到这一列中绝对值最大的一个元素,其对应行与主元行进行交换。交换之后作为新的主元。这样我们就能完全避免淹没问题。
同样,这样可以避免\(0\)主元问题。如果这一列没有非零元素,则矩阵是奇异矩阵,此时高斯消元怎样都不能得到正确解。
置换矩阵
定义1
置换矩阵是一个\(n\times n\)矩阵,其在每一行、每一列仅有一个\(1\),其他全部为\(0\)
置换矩阵基础定理
令\(P\)是通过对单位矩阵实施一组特定的行交换后得到的一个\(n\times n\)的置换矩阵,则对于任意的\(n\times n\)矩阵\(A\),\(PA\)对应于对矩阵\(A\)实施同样的行变换得到的结果。
例如
\[\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} \]
是由单位矩阵交换二三行得到的,则
\[\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} a & b & c\\ d & e & f \\ g & h & i \end{bmatrix}= \begin{bmatrix} a & b & c \\ g & h & i \\ d & e & f \end{bmatrix} \]
即把后面那个矩阵也交换了二三行。