[TOC]
向量代数与空间解析几何
方向角与方向余弦
非零向量\(\bold{r}\)与三条坐标轴的夹角\(\alpha\)、\(\beta\)、\(\gamma\)称为向量\(\bold{r}\)的方向角。设\(\overrightarrow{OM}=\bold{r}=(x,y,z)\),则有
\[(cos\alpha,cos\beta,cos\gamma)=\left(\frac{x}{|\bold{r}|},\frac{y}{|\bold{r}|},\frac{z}{|\bold{r}|}\right)=\frac{1}{|\bold{r}|}(x,y,z)=\frac{\bold{r}}{|\bold{r}|}=\bold{e} \]
\(cos\alpha,cos\beta,cos\gamma\)称为向量\(\bold{r}\)的方向余弦。并且有
\[cos^2\alpha+cos^2\beta+cos^2\gamma = 1 \]
数量积的运算规律
-
交换律 \(\bold{a}\cdot\bold{b}=\bold{b}\cdot\bold{a}\)
-
分配律 \((\bold{a+b})\cdot \bold{c}=\bold{a\cdot c+b\cdot c}\)
-
如下的结合律 \((\lambda \bold{a})\cdot\bold{b}=\lambda(\bold{a\cdot b})\),\(\lambda\)为数
向量积的运算规律
-
\(\bold{b\times a=-a\times b}\)
-
分配律 \(\bold{(a+b)\times c=a\times c+b\times c}\)
-
如下的结合律 \((\lambda \bold{a})\times \bold{b}=\lambda(\bold{a\times b})\),\(\lambda\)为数
平面的点法式方程
当平面\(\Pi\)上一点\(M_0(x_0,y_0,z_0)\)和它的一个法线向量\(\bold{n}=(A,B,C)\)已知时,有平面的点法式方程:
\[A(x-x_0)+B(y-y_0)+C(z-z_0)=0 \]
平面的一般方程
\[Ax+By+Cz+D=0 \]
其中这个平面的法向量为\(\bold{n}=(A,B,C)\)
平面的截距式方程
\[\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 \]
其中\(a,b,c\)分别为\(x,y,z\)轴上的截距
两平面夹角
\[cos\theta=\frac{|A_1A_2+B_1B_2+C_1C_2|}{\sqrt{A_1^2+B_1^2+C_1^2}\sqrt{A_2^2+B_2^2+C_2^2}} \]
点到平面距离公式
点\(P_0(x_0,y_0,z_0)\)到平面\(Ax+By+Cz+D=0\)的距离公式
\[d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} \]
空间直线的一般方程
\[\left\{\begin{matrix} A_1x+B_1y+C_1z+D_1=0\\ A_2x+B_2y+C_2z+D_2=0 \end{matrix}\right. \]
即两个平面的交线
另外两个平面的法向量的向量积可以算出直线的切向量
平面束方程
由上述空间直线方程可知,通过这一直线的平面还有
\[\lambda(A_1x+B_1y+C_1z+D_1)+\mu(A_2x+B_2y+C_2z+D_2)=0 \]
其中\(\lambda=1\)时
\[(A_1x+B_1y+C_1z+D_1)+\mu(A_2x+B_2y+C_2z+D_2)=0 \]
表示除了\(A_2x+B_2y+C_2z+D_2=0\),之外的过直线的平面束。
空间直线的对称式方程(点向式方程)
若已知直线过一点\(M_0(x_0, y_0, z_0)\)和它的一个方向向量\(\bold{s}=(m,n,p)\)。则有方程
\[\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p} \]
空间直线的参数方程
若设
\[\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}=t \]
则有
\[\left\{\begin{matrix} x=x_0+mt \\ y=y_0+nt \\ z=z_0+pt \end{matrix}\right. \]
两直线的夹角
设两直线方向向量分别为\(\bold{s_1}=(m_1,n_1,p_1)\)和\(\bold{s_2}=(m_2,n_2,p_2)\)
\[cos\varphi = \frac{|m_1m_2+n_1n_2+p_1p_2|}{\sqrt{m_1^2+n_1^2+p_1^2}\sqrt{m_2^2+n_2^2+p_2^2}} \]
直线与平面的夹角
设直线方向向量和平面法向量分别为\(\bold{s}=(m,n,p)\)和\(\bold{n}=(A,B,C)\)
\[sin\varphi = \frac{|Am+Bn+Cp|}{\sqrt{A^2+B^2+C^2}\sqrt{m^2+n^2+p^2}} \]
旋转曲面
设在\(yOz\)坐标面上有一已知曲线\(f(y,z)=0\)
则把这个曲线绕z轴旋转一周,得到的曲面为\(f(\pm\sqrt{x^2+y^2},z)=0\)
绕y轴旋转则为\(f(y,\pm\sqrt{x^2+z^2})=0\)
在其他坐标面上的曲线类似。
二次曲面举例
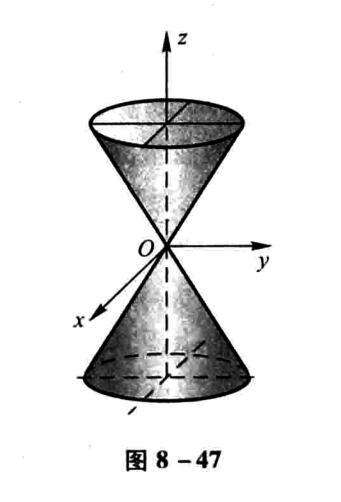
椭圆锥面
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=z^2 \]
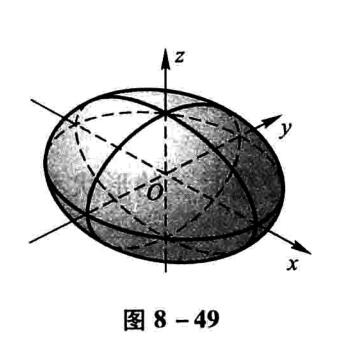
椭球面
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \]
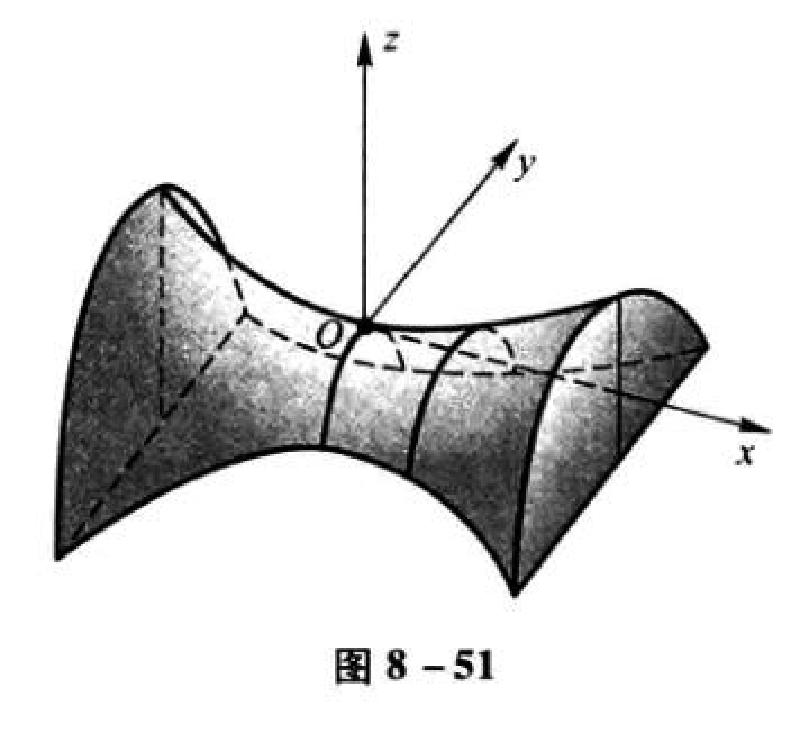
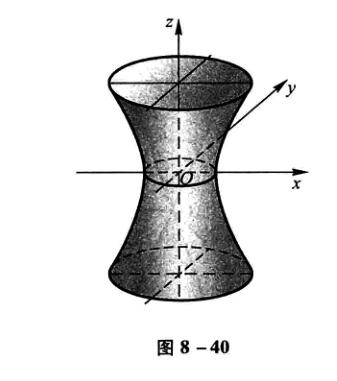
单叶双曲面
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1 \]
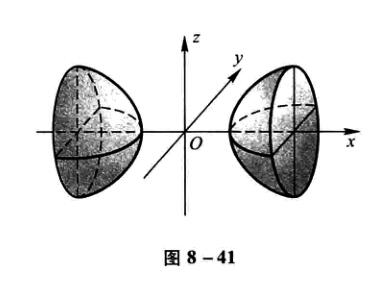
双叶双曲面
\[\frac{x^2}{a^2}-\frac{y^2}{b^2}-\frac{z^2}{c^2}=1 \]
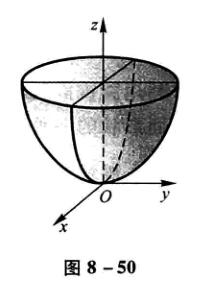
椭圆抛物面
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=z \]
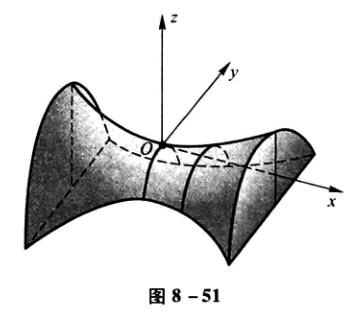
双曲抛物面
\[\frac{x^2}{a^2}-\frac{y^2}{b^2}=z \]
空间曲线及其方程
一般方程
即两个曲面的交线
\[\left\{\begin{matrix} F(x,y,z) = 0 \\ G(x,y,z) = 0 \end{matrix}\right. \]
参数方程
\[\left\{\begin{matrix} x=x(t) \\ y=y(t) \\ z=z(t) \end{matrix}\right. \]
多元函数微分法及其应用
多元函数的极限
注意极限存在,当且仅当从各个方向趋近那个点时得到的值存在并相等。
例如\(f(x,y)=\frac{xy}{x^2+y^2},x^2+y^2\neq 0;f(x,y)=0,x^2+y^2=0\),有沿x轴y轴趋近\((0,0)\)极限都为0,但沿直线\(y=kx\)趋近时极限随\(k\)变化。故极限不存在。
偏导数
注意有时利用定义求解偏导数会更优
例如关于\(x\)的偏导数
\[\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x} \]
在如\(x_0=0,y_0=0\)或者其他性质比较好的点,会更容易求。
高阶偏导数
-
注意分母上,求导顺序为从左到右。
-
如果函数\(z=f(x,y)\)的两个二阶混合偏导数\(\frac{\partial^2z}{\partial y\partial x}\)及\(\frac{\partial^2z}{\partial x\partial y}\)在区域\(D\)内连续,那么在该区域内这两个二阶混合偏导数必相等。
全微分
必要条件
如果函数\(z=f(x,y)\)在点\((x,y)\)可微分(蕴含着函数在该点上连续),那么该函数在点\((x,y)\)的偏导数\(\frac{\partial z}{\partial x}\)与\(\frac{\partial z}{\partial y}\)必定存在,且该函数在该点的全微分为
\[dz=\frac{\partial z}{\partial x}\Delta x+\frac{\partial z}{\partial y}\Delta y \]
但这只是必要条件。
形式上的全微分\(\Delta z\)(和上文的\(dz\)一个意思)应该满足
\[\frac{\Delta z-[f_x(x_0,y_0)\cdot\Delta x+f_y(x_0,y_0)\cdot\Delta y]}{\rho} \]
随着\(\rho\to0\)而趋于\(0\)。
其中
\[\rho=\sqrt{(\Delta x)^2+(\Delta y)^2} \]
才能可微。
充分条件
如果函数\(z=f(x,y)\)的偏导数\(\frac{\partial z}{\partial x}\)、\(\frac{\partial z}{\partial y}\)在\((x,y)\)连续,那么该函数在该点可微分。
多元复合函数的求导法则
一元函数与多元函数复合的情形
如果函数\(u=\varphi(t)\)及\(v=\psi(t)\)都在点\(t\)可导,函数\(z=f(u,v)\)在对应点\((u,v)\)具有连续偏导数,那么复合函数\(z=f[\varphi(t),\psi(t)]\)在t可导,且有
\[\frac{dz}{dt}=\frac{\partial z}{\partial u}\frac{du}{dt}+\frac{\partial z}{\partial v}\frac{dv}{dt} \]
多元函数与多元函数复合的情形
\[u=\varphi(x,y),v=\psi(x,y),z=f(u,v) \]
若都在对应点\((x,y)\)具有连续偏导数,则
\[\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial x} \]
\[\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial y} \]
混合复合
根据每个复合函数是否含有自变量\(x,y\)进行偏导,例如
\[u=\varphi(x,y),v=\psi(y),z=f(u,v) \]
则
\[\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x} \]
\[\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\frac{d v}{d y} \]
如果有两层复合函数,则要求导至将\(x,y\)这样的自变量暴露出来。
全微分形式的不变性
设函数\(z=f(u,v)\)具有连续偏导数,则有全微分
\[dz=\frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dv \]
若有\(u=\varphi(x,y),v=\psi(x,y)\),有
\[dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy \]
显然可以算出\(\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}\),代入有
\[dz=\frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dv \]
此为全微分形式的不变性。
隐函数的求导公式
一个方程的情形
\[F(x,y)=0 \]
\[\frac{dy}{dx}=-\frac{F_x}{F_y} \]
条件:F在某点的某一邻域内具有连续偏导数,\(F_y\)在该点不为0
\[F(x,y,z)=0 \]
\[\frac{\partial z}{\partial x}=-\frac{F_x}{F_z},\frac{\partial z}{\partial y}=-\frac{F_y}{F_z} \]
条件类似于上条。
方程组的情形
考虑如下方程组
\[\left\{\begin{matrix} F(x,y,u,v)=0\\ G(x,y,u,v)=0 \end{matrix}\right. \]
一般四个变量只能有两个变量独立变化
即
\[u(x,y),v(x,y) \]
两边应用求导法则得
\[F_x+F_u\frac{\partial u}{\partial x}+F_v\frac{\partial v}{\partial x}=0 \]
\[G_x+G_u\frac{\partial u}{\partial x}+G_v\frac{\partial v}{\partial x}=0 \]
解方程求出偏导数,求关于\(y\)的偏导数同理。
多元函数积分学的几何应用
一元向量值函数及其导数
空间曲线\(\Gamma\)的参数方程为
\[\left\{\begin{matrix} x=\varphi(t), \\ y=\psi(t), \\ z=\omega(t) \end{matrix}\right. t\in[\alpha,\beta] \]
写成向量形式,则为
\[\bold{r}=x\bold{i}+y\bold{j}+z\bold{k} \]
\[\bold{f}(t)=\varphi(t)\bold{i}+\psi(t)\bold{j}+\omega(t)\bold{k} \]
所以有\(\bold{r=f}(t)\), \(\bold{r}\)称为向量函数
向量值导数如下:
\[\bold{f}'(t_0)=\lim_{\Delta t\to 0}\frac{\Delta \bold{r}}{\Delta t} =\lim_{\Delta t\to 0}\frac{\bold{f}(t_0+\Delta t)-\bold{f}(t_0)}{\Delta t} \]
或者如下计算:
\[\bold{f}'(t_0)=\bold{f_1}'(t_0)\bold{i}+\bold{f_2}'(t_0)\bold j+ \bold{f_3}'(t_0)\bold k \]
空间曲线的切线与法平面
还是上面那个曲线\(\Gamma\),则切线方程为
\[\frac{x-x_0}{\varphi'(t_0)}= \frac{y-y_0}{\psi'(t_0)}= \frac{z-z_0}{\omega'(t_0)} \]
法平面方程为
\[\varphi'(t_0)(x-x_0)+ \psi'(t_0)(y-y_0)+ \omega'(t_0)(z-z_0)=0 \]
若\(\Gamma\)变为
\[\left\{\begin{matrix} x=x \\ y=\varphi(x) \\ z=\psi(x) \end{matrix}\right. \]
则切线方程变为
\[\frac{x-x_0}{1}= \frac{y-y_0}{\varphi'(x_0)}= \frac{z-z_0}{\psi'(x_0)} \]
法平面方程变为
\[(x-x_0)+ \varphi'(x_0)(y-y_0)+ \psi'(x_0)(z-z_0)=0 \]
曲线为方程组情形时(三个变量一般只有一个自由变量,所以直接将\(y,z\)替换为\(\varphi(x),\psi(x)\))
\[F[x,\varphi(x),\psi(x)]=0 \]
\[G[x,\varphi(x),\psi(x)]=0 \]
两边求对\(x\)的全导数
\[\frac{\partial F}{\partial x}+\frac{\partial F}{\partial y} \frac{dy}{dx}+\frac{\partial F}{\partial z}\frac{dz}{dx}=0 \]
\[\frac{\partial G}{\partial x}+\frac{\partial G}{\partial y} \frac{dy}{dx}+\frac{\partial G}{\partial z}\frac{dz}{dx}=0 \]
解出\(\bold{T}=(1,\frac{dy}{dx},\frac{dz}{dx})\),即\(\bold{T}=(1,\varphi'(x_0),\psi'(x_0))\),就是在此点的切向量,代入可知切线与法平面方程
曲面的切平面与法线
若曲面由\(F(x,y,z)=0\)隐性给出,则在点\(M(x_0,y_0,z_0)\)切平面方程为
\[F_x(x-x_0)+F_y(y-y_0)+F_z(z-z_0)=0 \]
其中各个偏导数都是在M点的偏导数,法线方程如下
\[\frac{x-x_0}{F_x}=\frac{y-y_0}{F_y}=\frac{z-z_0}{F_z} \]
考虑曲面方程为\(z=f(x,y)\),则可令\(F(x,y,z)=f(x,y)-z\)
显然有
\[F_x(x,y,z)=f_x(x,y),F_y(x,y,z)=f_y(x,y),F_z(x,y,z)=-1 \]
切平面、法线方程类似于上。
方向导数与梯度
方向导数:
\[\frac{\partial f}{\partial l}\bigg|_{(x_0,y_0)}= \lim _{t\to 0^+}\frac{f(x_0+tcos\alpha,y_0+tcos\beta)-f(x_0,y_0)}{t} \]
如果函数\(f(x,y)\)在点\(P_0(x_0,y_0)\)可微分,那么函数在该点沿任一方向\(l\)的方向导数存在,且有
\[\frac{\partial f}{\partial l}\bigg|_{(x_0,y_0)}= f_x(x_0,y_0)cos\alpha+f_y(x_0,y_0)cos\beta \]
其中\(cos\alpha,cos\beta\)是方向\(l\)的方向余弦。
梯度:
\[\bold{grad}f(x_0,y_0)=\nabla f(x_0,y_0)=f_x(x_0,y_0)\bold{i}+ f_y(x_0,y_0)\bold{j} \]
如果方向导数存在,则
\[\frac{\partial f}{\partial l}\bigg|_{(x_0,y_0)}= f_x(x_0,y_0)cos\alpha+f_y(x_0,y_0)cos\beta =\nabla f(x_0,y_0)\cdot \bold{e}_l=|\nabla f|cos\theta \]
其中
\[\theta=<\nabla f,\bold{e}_l> \]
多元函数的极值及其求法
必要条件
设函数\(z=f(x,y)\)在点\((x_0,y_0)\)具有偏导数,且在点\((x_0,y_0)\)处有极值,则有
\[f_x(x_0,y_0)=0,f_y(x_0,y_0)=0 \]
充分条件
设函数\(z=f(x,y)\)在点\((x_0,y_0)\)的某领域内连续且有一阶和二阶连续偏导数,又\(f_x(x_0,y_0)=0,f_y(x_0,y_0)=0\),令
\[f_{xx}(x_0,y_0)=A,f_{xy}(x_0,y_0)=B,f_{yy}(x_0,y_0)=C \]
若
-
\(AC-B^2>0\)时具有极值,\(A<0\)时有极大值,\(A>0\)时有极小值;
-
\(AC-B^2<0\)时没有极值
-
\(AC-B^2=0\)时可能有也可能没有,需要另作讨论。
拉格朗日乘数法
要找函数\(z=f(x,y)\)在附加条件\(\varphi(x,y)=0\)下的可能极值点,先设
\[L(x,y)=f(x,y)+\lambda\varphi(x,y) \]
令
\[\left\{\begin{matrix} L_x=f_x+\lambda\varphi_x=0 \\ L_y=f_y+\lambda\varphi_y=0 \\ L_{\lambda}=\varphi=0 \end{matrix}\right. \]
解出\(x,y,\lambda\),代入函数\(f\)中求得可能的极值点。
多个条件时,如多加一个\(\psi(x,y)=0\),则设方程
\[L(x,y)=f(x,y)+\lambda\varphi(x,y)+\mu\psi(x,y) \]
分别求\(L_x=0,L_y=0,L_\lambda=0,L\mu=0\),代入原函数中求可能的极值点。
重积分
二重积分的概念与性质
性质:
- 设\(\alpha,\beta\)为常数,则
\[\iint\limits_{D}[\alpha f(x,y)+\beta g(x,y)]d\sigma= \alpha\iint\limits_{D}f(x,y)d\sigma+\beta\iint\limits_{D}g(x,y)d\sigma \]
- 如果闭区域\(D\)被有限条曲线分为有限个部分闭区域,那么在\(D\)上的二重积分等于在各部分闭区域上的二重积分的和
\[\iint\limits_{D}f(x,y)d\sigma= \iint\limits_{D_1}f(x,y)d\sigma+\iint\limits_{D_2}f(x,y)d\sigma \]
- 如果在\(D\)上,\(f(x,y)=1\),\(\sigma\)为\(D\)的面积,那么
\[\sigma=\iint\limits_{D}1\cdot d\sigma=\iint\limits_{D}d\sigma \]
- 如果在\(D\)上,\(f(x,y)\leq g(x,y)\),那么有
\[\iint\limits_{D}f(x,y)d\sigma\leq\iint\limits_{D}g(x,y)d\sigma \]
特别的,有
\[\left|\iint\limits_{D}f(x,y)d\sigma\right|\leq \iint\limits_{D}|f(x,y)|d\sigma \]
- 设\(M\)和\(N\)分别是\(f(x,y)\)在闭区域\(D\)上的最大值和最小值,\(\sigma\)是\(D\)的面积,则有
\[m\sigma\leq\iint\limits_{D}f(x,y)d\sigma\leq M\sigma \]
- 设函数\(f(x,y)\)在闭区域D上连续,\(\sigma\)是\(D\)的面积,则在\(D\)上至少存在一点\((\xi,\eta)\),使得
\[\iint\limits_{D}f(x,y)d\sigma=f(\xi,\eta)\sigma \]
二重积分的计算法
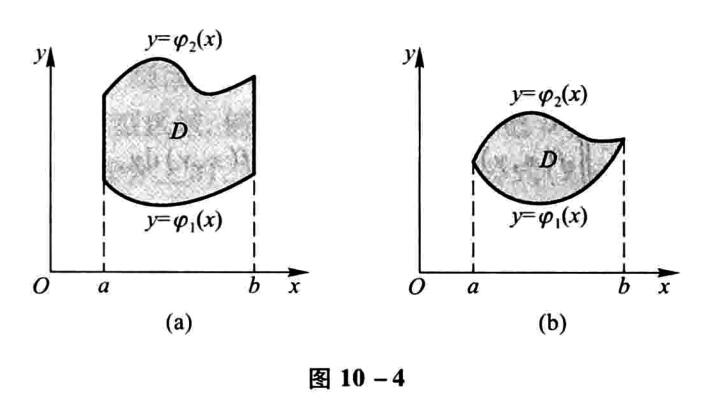
利用直角坐标计算二重积分
在如图的区域中,积分上限为上方曲线,积分下限为下方曲线。
\[\iint\limits_{D}f(x,y)d\sigma=\int_a^bdx\int_{\varphi_1(x)} ^{\varphi_2(x)}f(x,y)dy \]
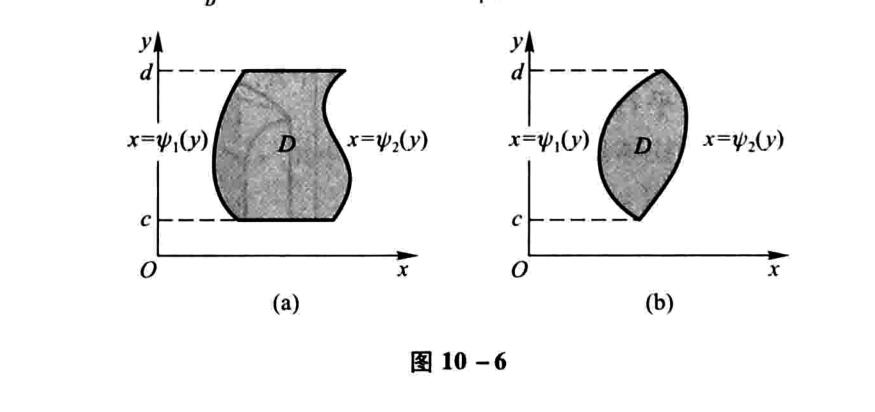
如图则,积分上限为右侧曲线,下限为左侧曲线。
\[\iint\limits_{D}f(x,y)d\sigma=\int_c^ddy\int_{\psi_1(y)} ^{\psi_2(y)}f(x,y)dx \]
利用极坐标计算二重积分
有
\[x=\rho cos\theta \]
\[y=\rho sin\theta \]
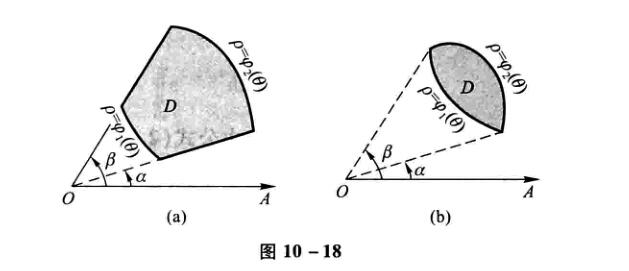
且有对于下图
\[\iint\limits_{D}f(x,y)d\sigma=\iint\limits_{D}f(\rho cos\theta, \rho sin\theta)\rho d\rho d\theta \]
\[=\int_\alpha^\beta d\theta\int_{\varphi_1(\theta)} ^{\varphi_2(\theta)}f(\rho cos\theta, \rho sin\theta)\rho d\rho \]
三重积分的计算
利用直角坐标计算三重积分
- “先1后2法”,即先以\(z\)为积分变量计算
\[\iiint\limits_\Omega f(x,y,z)dv=\int_a^bdx\int_{y_1(x)}^{y_2(x)} dy\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)dz \]
- “先2后1法”,即先以\(xy\)为积分变量计算
\[\iiint\limits_\Omega f(x,y,z)dv=\int_{c_1}^{c_2}dz\iint\limits_{D_z} f(x,y,z)dxdy \]
利用柱面坐标计算
有
\[\left\{\begin{matrix} x=\rho cos\theta \\ y=\rho sin\theta \\ z=z \end{matrix}\right. \]
有
\[\iiint\limits_{\Omega}f(x,y,z)dxdydz= \iiint\limits_{\Omega}F(\rho,\theta,z)\rho d\rho d\theta dz \]
利用球面坐标计算
有
\[\left\{\begin{matrix} x=rsin\varphi cos\theta \\ y=rsin\varphi sin\theta \\ z=rcos\varphi \end{matrix}\right. \]
有
\[\iiint\limits_{\Omega}f(x,y,z)dxdydz= \iiint\limits_{\Omega}F(r,\varphi,\theta)r^2sin\varphi drd\varphi d\theta \]
拆分被积函数
详细的证明没有在书中和老师的教学中找到,互联网搜索也较难
书上有许多例子,如当
\[\rho ^2\leq z\leq4,0\leq\rho\leq2,0\leq\theta\leq2\pi \]
有
\[\iiint\limits_{\Omega}zdxdydz=\iiint\limits_{\Omega}z\rho d\rho d\theta dz=\int_0^{2\pi}d\theta\int_0^2\rho d\rho\int_{\rho^2}^4zdz \]
推断为,首先被积函数要是\(f(z)g(\rho)\)等用乘法连接的,如\(z\rho\),而不能是加法如\(z+\rho\),才能拆分。另外跟积分上下限的关系不明。
如果是加法,如\(x+y+z\)可以从轮换对称性考虑(如果有)
重积分的应用
曲面面积
设曲面为\(z=f(x,y)\),则
\[A=\iint\limits_D\sqrt{1+f_x^2(x,y)+f_y^2(x,y)}dxdy \]
质心
设有一平面薄片,占据\(xOy\)面上的闭区域\(D\),在点\((x,y)\)处的面密度为\(\mu(x,y)\)
则有
\[M_y=\iint\limits_Dx\mu(x,y)d\sigma, M_x=\iint\limits_Dy\mu(x,y)d\sigma \]
\[M=\iint\limits_D\mu(x,y)d\sigma \]
质心坐标为
\[\bar{x}=\frac{M_y}{M}= \frac{\iint\limits_Dx\mu(x,y)d\sigma}{\iint\limits_D\mu(x,y)d\sigma} \]
\[\bar{y}=\frac{M_x}{M}=\frac{\iint\limits_Dy\mu(x,y)d\sigma}{\iint\limits_D\mu(x,y)d\sigma} \]
转动惯量
\[I_x=\iint\limits_Dy^2\mu(x,y)d\sigma,I_y=\iint\limits_Dx^2\mu(x,y)d\sigma \]
引力
空间一物体对物体外一点\(P_0(x_0,y_0,z_0)\)的单位质量的质点的引力
物体密度\(\rho(x,y,z)\),
\[\bold{F}=(F_x,F_y,F_z) \]
\[=\left ( \iiint\limits_\Omega\frac{G\rho(x,y,z)(x-x_0)}{r^3}dv, \iiint\limits_\Omega\frac{G\rho(x,y,z)(y-y_0)}{r^3}dv, \iiint\limits_\Omega\frac{G\rho(x,y,z)(z-z_0)}{r^3}dv \right ) \]
曲线积分与曲面积分
对弧长的曲线积分
性质
- 设\(\alpha,\beta\)为常数,则
\[\int_L[\alpha f(x,y)+\beta g(x,y)]ds=\alpha\int_L f(x,y)ds+\beta \int_Lg(x,y)ds \]
- 若积分弧段\(L\)课分成两段光滑曲线弧\(L_1\)和\(L_2\),则
\[\int_Lf(x,y)ds=\int_{L_1}f(x,y)ds+\int_{L_2}f(x,y)ds \]
- 设在\(L\)上\(f(x,y)\leq g(x,y)\), 则
\[\int_L f(x,y)ds\leq\int_L g(x,y)ds \]
特别地,有
\[\left|\int_L f(x,y)ds\right|\leq\int_L|f(x,y)|ds \]
对弧长的曲线积分的计算法
设\(f(x,y)\)在曲线弧\(L\)上有定义且连续,\(L\)的参数方程为
\[\left\{\begin{matrix} x=\varphi(t) \\ y=\psi(t) \end{matrix}\right. (\alpha\leq t\leq\beta) \]
若\(\varphi(t)\)、\(\psi(t)\)在\([\alpha,\beta]\)上具有一阶连续导数,且\(\varphi'^2(t)+\psi'^2(t)\neq0\),则曲线积分\(\int_Lf(x,y)ds\)存在,且
\[\int_Lf(x,y)ds=\int_\alpha^\beta f[\varphi(t),\psi(t)] \sqrt{\varphi'^2(t)+\psi'^2(t)}dt (a<\beta) \]
注意\(\alpha<\beta\)是一定要有的。
对坐标的曲线积分
\[\int_LP(x,y)dx+Q(x,y)dy \]
也可以写作向量形式
\[\int_L\bold{F(x,y)}\cdot d\bold{r} \]
其中\(\bold{F}=P\bold{i}+Q\bold{j}\),\(d\bold{r}=dx\bold{i}+dy\bold{j}\).
性质
-
与上节相同
-
与上节相同
-
设\(L\)是有向光滑曲线弧,\(L^-\)是\(L\)的反向曲线弧,则
\[\int_{L^-}\bold F(x,y)d\bold r = -\int_L\bold F(x,y)d\bold r \]
对坐标的曲线积分的计算方法
条件相似,不再重复,查阅书籍
\[\left\{\begin{matrix} x=\varphi(t) \\ y=\psi(t) \end{matrix}\right. \]
\(t\)单调地由\(\alpha\)变到\(\beta\)
\[\int_LP(x,y)dx+Q(x,y)dy \]
\[=\int_\alpha^\beta\{P[\varphi(t),\psi(t)]\varphi'(t)+ Q[\varphi(t),\psi(t)]\psi'(t)\}dt \]
不需要\(\alpha<\beta\),有时有\(x=x,y=y(x)\),类似的替换公式即可。
两类曲线积分之间的联系
\[\int_LPdx+Qdy=\int_L(Pcos\alpha+Qcos\beta)ds \]
易推广至三维
也可以写成向量形式
\[\int_L\bold A\cdot d\bold r = \int_L\bold A\cdot\bm{\tau}ds= \int_LA_{\tau}ds \]
格林公式
定理1,设闭区域\(D\)由分段光滑的曲线\(L\)围成,若函数\(P(x,y)\)及\(Q(x,y)\)在\(D\)上具有一阶连续偏导数,则有
\[\iint\limits_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}) dxdy=\oint_LPdx+Qdy \]
其中\(L\)是\(D\)的取正向的边界曲线。
对平面区域\(D\)的边界曲线\(L\),规定正向如下:当观察者沿着\(L\)的这个方向行走时,\(D\)总在他的左边。
定理2,设区域\(G\)是一个单连通域(复连通不是充要条件),若函数\(P(x,y),Q(x,y)\)在\(G\)内具有一阶连续偏导数,则曲线积分\(\int_LPdx+Qdy\)在\(G\)内与路径无关(或沿着\(G\)内任意闭曲线的曲线积分为0)的充分必要条件是
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x} \]
在\(G\)内恒成立。
定理3,设区域\(G\)是一个单连通域(复连通不是充要条件,若函数\(P(x,y),Q(x,y)\)在\(G\)内具有一阶连续偏导数,则\(P(x,y)dx+Q(x,y)dy\)在\(G\)内为某一函数\(u(x,y)\)的全微分的充分必要条件是
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x} \]
在\(G\)内恒成立。
对面积的曲面积分
\[\iint\limits_{\Sigma}f(x,y,z)dS \]
\[=\iint\limits_{D_{xy}}f[x,y,z(x,y)]\sqrt{1+z_x^2(x,y)+z_y^2(x,y)}dxdy \]
对坐标的曲面积分
关于方向
假设某块小曲面\(\Delta S\)与\(z\)轴的夹角为\(\gamma\)角,在\(xOy\)面上的投影是\((\Delta\sigma)_{xy}\),则规定\(\Delta S\)在\(xOy\)面上的投影\((\Delta S)_{xy}\)为
\[(\Delta S)_{xy}=\left\{\begin{matrix} (\Delta\sigma)_{xy}, cos\gamma>0 \\ -(\Delta\sigma)_{xy}, cos\gamma<0 \\ 0, cos\gamma\equiv 0 \end{matrix}\right. \]
投影到其他坐标面类似,总而言之向上、向右、向前是正向曲面。
对坐标的曲面积分的计算法
如果曲面积分是在曲面\(\Sigma\)上侧的,那么
\[\iint\limits_\Sigma R(x,y,z)dxdy=\iint\limits_{D_{xy}}R[x,y,z(x,y)]dxdy \]
若在下侧,则
\[\iint\limits_\Sigma R(x,y,z)dxdy=-\iint\limits_{D_{xy}}R[x,y,z(x,y)]dxdy \]
同理有
\[\iint\limits_\Sigma P(x,y,z)dydz=\pm\iint\limits_{D_{yz}}P[x(y,z),y,z]dydz \]
\[\iint\limits_\Sigma Q(x,y,z)dzdx=\pm\iint\limits_{D_{zx}}Q[x,y(z,x),z]dzdx \]
两类曲面积分之间的联系
\[\iint\limits_\Sigma Pdydz+Qdzdx+Rdxdy=\iint\limits_\Sigma(Pcos\alpha+Qcos\beta+Rcos\gamma)dS \]
写成向量形式
\[\iint\limits_\Sigma \bold{A}\cdot d\bold{S}=\iint\limits_\Sigma \bold{A}\cdot\bold{n}dS \]
高斯公式 通量与散度
高斯公式
设空间闭区域\(\Omega\)是由分片光滑的闭曲面\(\Sigma\)所围成,若函数\(P(x,y,z),Q(x,y,z),R(x,y,z)\)在\(\Omega\)上具有一阶连续偏导数,则有
\[\iiint\limits_\Omega(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dv=\oiint\limits_\Sigma Pdydz+Qdzdx+Rdxdy \]
或
\[\iiint\limits_\Omega(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dv=\oiint\limits_\Sigma(Pcos\alpha+Qcos\beta+Rcos\gamma)dS \]
这里\(\Sigma\)是\(\Omega\)的整个边界曲面的外侧,\(cos\alpha、cos\beta、cos\gamma\)是\(\Sigma\)在点\((x,y,z)\)处的法向量的方向余弦。
沿任意闭曲面的曲面积分为零的条件
设\(G\)是空间二维单连通区域,若\(P(x,y,z),Q(x,y,z),R(x,y,z)\)在\(G\)内具有一阶连续偏导数,则曲面积分
\[\iint\limits_\Sigma Pdydz+Qdzdx+Rdxdy \]
在\(G\)内所取曲面\(\Sigma\)无关而只取决于\(\Sigma\)的边界曲线(或沿\(G\)内任一闭曲面的曲面积分为零)的充分必要条件是
\[\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=0 \]
在\(G\)内恒成立。
通量与散度
设有向量场
\[\bold{A}(x,y,z) = P(x,y,z)\bold i+Q(x,y,z)\bold j+R(x,y,z)\bold k \]
其中函数\(P,Q,R\)均有一阶连续偏导数,\(\Sigma\)是场内的一片有向曲面,\(\bold n\)是\(\Sigma\)在点\((x,y,z)\)处的单位法向量,则积分
\[\iint\limits_\Sigma \bold A\cdot \bold ndS \]
称为向量场\(\bold A\)通过曲面\(\Sigma\)向着指定侧的通量(或流量)。 又可表达为
\[\iint\limits_\Sigma \bold A\cdot \bold ndS=\iint\limits_\Sigma \bold Ad\bold S=\iint\limits_\Sigma Pdydz+Qdzdx+Rdxdy \]
对于这个向量场,其散度记作\(div\bold A\),即
\[div\bold A=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z} \]
利用向量微分算子\(\nabla\),也可以表示为
\[div\bold A = \nabla\cdot\bold A \]
利用向量场的通量和散度,高斯公式可以写成
\[\iiint\limits_{\Omega}div\bold Adv=\iint\limits_\Sigma A_ndS \]
斯托克斯公式 环流量与旋度
斯托克斯公式
设\(\Gamma\)为分段光滑的空间有向闭曲线,\(\Sigma\)是以\(\Gamma\)为边界的分片光滑的有向曲面,\(\Gamma\)的正向与\(\Sigma\)的侧符合右手规则,若函数\(P(x,y,z),Q(x,y,z),R(x,y,z)\)在曲面\(\Sigma\)(连同边界\(\Gamma\))上具有一阶连续偏导数,则有
\[\iint\limits_\Sigma\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)dydz+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)dzdx+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)dxdy \]
\[=\oint_\Gamma Pdx+Qdy+Rdz \]
空间曲线积分与路径无关的条件
设空间区域\(G\)是一维单连通域,若函数\(P(x,y,z),Q(x,y,z),R(x,y,z)\)在\(G\)内具有一阶连续偏导数,则空间曲线积分\(\int_\Gamma Pdx+Qdy+Rdz\)在\(G\)内与路径无关(或沿\(G\)内任意闭合曲线的曲线积分为零)的充分必要条件是
\[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x},\frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y},\frac{\partial R}{\partial x}=\frac{\partial P}{\partial z} \]
在\(G\)内恒成立
环流量与旋度
设有向量场
\[\bold{A}(x,y,z) = P(x,y,z)\bold i+Q(x,y,z)\bold j+R(x,y,z)\bold k \]
其中函数\(P,Q,R\)均连续,\(\Gamma\)是\(\bold A\)的定义域内的一条分段光滑的有向闭曲线,\(\bm\tau\)是\(\Gamma\)在点\((x,y,z)\)处的单位切向量,则积分
\[\oint_L\bold A\cdot\bm {\tau}ds \]
称为向量场\(\bold A\)沿有向闭曲线\(\Gamma\)的环流量。
又可表述为
\[\oint_L\bold A\cdot\bm {\tau}ds=\oint_L\bold Ad\bold r = \oint_\Gamma Pdx+Qdy+Rdz \]
向量场\(\bold A\)的旋度,记作\(\bold{rotA}\),即
\[\bold{rotA} = \left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\bold i+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\bold j+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\bold k \]
\[\bold{rotA}=\nabla\times\bold A \]
同样的,斯托克斯公式可以写成
\[\iint\limits_\Sigma\bold{rotA}\cdot\bold{n}dS=\oint_\Gamma\bold{A}\cdot\bm{\tau}ds \]
\[\iint\limits_\Sigma(\bold{rotA})_ndS=\oint_{\Gamma}\bold{A}_{\tau} ds \]
无穷级数
常数项级数的概念和性质
常数项级数的概念
如果级数\(\sum^{\infty}_{i=1}u_i\)的部分和数列\(\{s_n\}\)有极限s,即
\[\lim\limits_{n\to\infty}s_n=s \]
那么称无穷级数\(\sum^{\infty}_{i=1}u_i\)收敛,这时极限\(s\)叫做这级数的和,并写成
\[s=u_1+u_2+\dots+u_n+\cdots \]
如果\(\{s_n\}\)没有极限,那么称无穷级数\(\sum^{\infty}_{i=1}u_i\)发散
收敛级数的基本性质
性质1 如果级数\(\sum^{\infty}_{n=1}u_n\)收敛于和\(s\),那么级数\(\sum^{\infty}_{i=1}ku_i\)也收敛,且其和为\(ks\).
性质2 如果级数\(\sum^{\infty}_{n=1}u_n\)与\(\sum^{\infty}_{n=1}v_n\)分别收敛于\(s,\sigma\),那么级数\(\sum^{\infty}_{n=1}(u_n\pm v_n)\)也收敛,且其和为\(s\pm\sigma\)
性质3 在级数中去掉、加上或改变有限项,不会改变级数的收敛性
性质4 如果级数\(\sum^{\infty}_{n=1}u_n\)收敛,那么对于这级数的项任意加括号后所成的级数仍收敛,且其和不变
性质5(级数收敛的必要条件) 如果级数\(\sum^{\infty}_{n=1}u_n\)收敛,那么它的一般项\(u_n\)趋于0,即
\[\lim\limits_{n\to\infty}u_n=0 \]
常数项级数的审敛法
正项级数及其审敛法
定理1 正项级数\(\sum^{\infty}_{n=1}u_n\)收敛的充分必要条件是:它的部分和数列\(\{s_n\}\)有界
定理2(比较审敛法) 设\(\sum^{\infty}_{n=1}u_n\)和\(\sum^{\infty}_{n=1}v_n\)都是正项级数,且\(u_n\leq v_n\).若级数\(\sum^{\infty}_{n=1}v_n\)收敛,则级数\(\sum^{\infty}_{n=1}u_n\)收敛,若级数\(\sum^{\infty}_{n=1}u_n\)发散,则级数\(\sum^{\infty}_{n=1}v_n\)发散.
推论 设\(\sum^{\infty}_{n=1}u_n\)和\(\sum^{\infty}_{n=1}v_n\)都是正项级数,如果级数\(\sum^{\infty}_{n=1}v_n\)收敛,且存在正整数\(N\)使当\(n\ge N\)时有\(u_n\leq kv_n(k>0)\)成立,那么级数\(\sum^{\infty}_{n=1}u_n\)收敛;如果级数\(\sum^{\infty}_{n=1}v_n\)发散,且存在正整数\(N\)使当\(n\ge N\)时有\(u_n\ge kv_n(k>0)\)成立,那么级数\(\sum^{\infty}_{n=1}u_n\)发散.
定理3(比较审敛法的极限形式) 设\(\sum^{\infty}_{n=1}u_n\)和\(\sum^{\infty}_{n=1}v_n\)都是正项级数,
- 如果\(\lim\limits_{n\to\infty}\frac{u_n}{v_n}=l(0\leq l<+\infty)\),且级数\(\sum^{\infty}_{n=1}v_n\)收敛,那么级数\(\sum^{\infty}_{n=1}u_n\)收敛;
- 如果\(\lim\limits_{n\to\infty}\frac{u_n}{v_n}=l>0\)或\(\lim\limits_{n\to\infty}\frac{u_n}{v_n}=+\infty\),且级数\(\sum^{\infty}_{n=1}v_n\)发散,那么级数\(\sum^{\infty}_{n=1}u_n\)发散;
定理4(比值审敛法,达朗贝尔判别法) 设\(\sum^{\infty}_{n=1}u_n\)是正项级数,如果
\[\lim\limits_{n\to\infty}\frac{u_{n+1}}{u_n}=\rho \]
那么当\(\rho<1\)时级数收敛,\(\rho>1\)(或\(\lim\limits_{n\to\infty}\frac{u_{n+1}}{u_n}=\infty\))时级数发散,\(\rho=1\)时级数可能收敛也可能发散。
定理5(根值审敛法,柯西判别法) 设\(\sum^{\infty}_{n=1}u_n\)是正项级数,如果
\[\lim\limits_{n\to\infty}\sqrt[n]{u_n}=\rho \]
那么当\(\rho<1\)时级数收敛,\(\rho>1\)(或\(\lim\limits_{n\to\infty}\sqrt[n]{u_n}=+\infty\))时级数发散,\(\rho=1\)时级数可能收敛也可能发散。
定理6(极限审敛法) \(\sum^{\infty}_{n=1}u_n\)是正项级数,
- 如果\(\lim\limits_{n\to\infty}nu_n=l>0\)(或\(\lim\limits_{n\to\infty}nu_n=+\infty\)),那么该级数发散;
- 如果\(p>1\),而\(\lim\limits_{n\to\infty}n^pu_n=l>0(0\leq l<+\infty)\),那么该级数收敛.
交错级数及其审敛法
定理7(莱布尼茨定理) 如果交错级数\(\sum^{\infty}_{n=1}(-1)^{n-1}u_n\)满足条件:
- \(u_n\ge u_{n+1}\)
- \(\lim\limits_{n\to\infty}u_n=0\)
那么级数收敛,且其和\(s\leq u_1\),其余项\(r_n\)的绝对值小于等于\(u_{n+1}\)
绝对收敛与条件收敛
对于级数\(\sum^{\infty}_{n=1}u_n\),若\(\sum^{\infty}_{n=1}|u_n|\)收敛,那么称\(\sum^{\infty}_{n=1}u_n\)绝对收敛;如果\(\sum^{\infty}_{n=1}u_n\)收敛,而\(\sum^{\infty}_{n=1}|u_n|\)发散,则成\(\sum^{\infty}_{n=1}u_n\)条件收敛。
定理8 如果级数\(\sum^{\infty}_{n=1}u_n\)绝对收敛,那么\(\sum^{\infty}_{n=1}u_n\)必定收敛。
绝对收敛级数的性质
定理9 绝对收敛级数经改变项的位置后构成的级数也收敛,且与原级数有相同的和.
定理10 (绝对收敛级数的乘法) 设\(\sum^{\infty}_{n=1}u_n\)和\(\sum^{\infty}_{n=1}v_n\)都是绝对收敛,其和分别为\(s,\sigma\),则它们的柯西乘积
\[u_1v_1+(u_1v_2+u_2v_1)+\dots+(u_1v_n+u_2v_{n-1}+\dots+u_nv_1)+\cdots \]
也是绝对收敛的,且其和为\(s\sigma\)
幂级数
收敛域:开区间;收敛区间:要判断边界点
定理1(阿贝尔定理) 如果级数\(\sum^{\infty}_{n=0}a_nx^n\)当\(x=x_0\neq0\)时收敛,那么适合不等式\(|x|<|x_0|\)的一切\(x\)使这幂级数绝对收敛,反之,如果级数\(\sum^{\infty}_{n=0}a_nx^n\)当\(x=x_0\neq0\)当\(x=x_0\)时发散,那么适合不等式\(|x|>|x_0|\)的一切\(x\)使这幂级数发散.
推论 如果幂级数\(\sum^{\infty}_{n=0}a_nx^n\)不仅在\(x=0\)一点收敛,也不是在整个数轴上都收敛,那么必有一个确定的正数\(R\)存在,使得
当\(|x|< R\)时,幂级数绝对收敛
当\(|x|>R\)时,幂级数发散
当\(|x|=R\)时,幂级数可能收敛也可能发散,如果收敛可能是绝对或条件收敛。
正数\(R\)通常叫做收敛半径。
定理2 如果
\[\lim\limits_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|=\rho \]
其中\(a_n,a_{n+1}\)是幂级数\(\sum^{\infty}_{n=0}a_nx^n\)的相邻两项的系数,那么这幂级数的收敛半径
\[R=\left\{\begin{matrix} \frac{1}{\rho}, \rho\ne0\\ +\infty, \rho=0 \\ 0, \rho=+\infty \end{matrix}\right. \]
注意如果级数的项中为\(x^{2n}\)等不能化为\(x^n\)的,不能用这个定理,只能用比值审敛法等通用手段。
幂级数的运算
设\(\sum^{\infty}_{n=0}a_nx^n\)和\(\sum^{\infty}_{n=0}b_nx^n\)分别在区间\((-R,R),(-R',R')\)内收敛,则对于这两个幂级数,
- \(\sum^{\infty}_{n=0}a_nx^n\pm\sum^{\infty}_{n=0}b_nx^n=\sum^{\infty}_{n=0}(a_n\pm b_n)x^n\)在\((-R,R),(-R',R')\)中较小的区间内成立.
- \(\sum^{\infty}_{n=0}a_nx^n\sum^{\infty}_{n=0}b_nx^n=a_0b_0+(a_0b_1+a_1b_0)x+\dots+(a_0b_n+a_1b_{n-1}+\dots+a_nb_0)x^n+\cdots\),\((-R,R),(-R',R')\)中较小的区间内成立.
- \(\frac{\sum^{\infty}_{n=0}a_nx^n}{\sum^{\infty}_{n=0}b_nx^n}=\sum^{\infty}_{n=0}c_nx^n\),假设\(b_0\ne0\),\(c\)可以由下式求出
\[a_0=b_0c_0\\ a_1=b_1c_0+b_0c_1\\ a_2=b_2c_0+b_1c_1+b_0c_2\\ \cdots \]
幂级数\(\sum^{\infty}_{n=0}c_nx^n\)的收敛区间可能比原来两级数的收敛区间小得多。
幂级数的和函数的性质
性质1 幂级数\(\sum^{\infty}_{n=0}a_nx^n\)的和函数\(s(x)\)在其收敛域\(I\)上连续
性质2 幂级数\(\sum^{\infty}_{n=0}a_nx^n\)的和函数\(s(x)\)在其收敛域\(I\)上可积,并有逐项积分公式
\[\int_0^xs(x)dt=\int_0^x[\sum^{\infty}_{n=0}a_nt^n]dt=\sum^{\infty}_{n=0}\int_0^xa_nt^ndt=\sum^{\infty}_{n=0}\frac{a_n}{n+1}x^{n+1}(x\in I), \]
逐项积分后所得到的幂级数和原级数有相同的收敛半径。
性质3 幂级数\(\sum^{\infty}_{n=0}a_nx^n\)的和函数\(s(x)\)在其收敛域\(I\)上可导,且有逐项求导公式
\[s'(x)=(\sum^{\infty}_{n=0}a_nx^n)'=\sum^{\infty}_{n=0}(a_nx^n)'=\sum^{\infty}_{n=1}na_nx^{n-1} \]
逐项求导后所得到的幂级数和原级数有相同的收敛半径.
反复应用上述结论可得:\(s(x)\)在其收敛区间\((-R,R)\)内具有任意阶导数。
函数展开成幂级数
泰勒级数和麦克劳林级数不再重复,见上册整理。
\(f(x)\)能在某个邻域展开成泰勒级数的充要条件是
\[\lim\limits_{n\to\infty}R_n(x)=0, x\in U(x_0) \]
除了直接展开外,通常也会有间接展开的办法。即通过四则运算、求导、积分、变量替换等等运算转化为一些常见的函数,再代入这些常见函数的展开式。
下面给出一些常见函数的展开式
\[\frac{1}{1-x}=\sum_{n=0}^{\infty}x^n,x\in(-1,1) \]
\[\frac{1}{1+x}=\sum_{n=0}^{\infty}(-1)^nx^n,x\in(-1,1) \]
\[e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!},x\in(-\infty,\infty) \]
\[sinx=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}x^{2n+1},x\in(-\infty,\infty) \]
\[cosx=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n)!}x^{2n},x\in(-\infty,\infty) \]
\[ln(1+x)=\sum_{n=0}^{\infty}\frac{(-1)^n}{n+1}x^{n+1}= \sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}x^{n},x\in(-1,1] \]
\[(1+x)^m=1+mx+\frac{m(m-1)}{2!}x^2+\cdots+\frac{m(m-1)\cdots(m-n+1)}{n!}x^n+\cdots \]
傅里叶级数
一个定义在\((-\infty,\infty)\)上周期为\(2\pi\)的函数\(f(x)\),如果它在一个周期上可积,那么一定可以做出\(f(x)\)的傅里叶级数
\[f(x) = \frac{a_0}{2}+\sum_{n=1}^{\infty}(a_ncosnx+b_nsinnx) \]
其中
\[a_n=\frac{1}{\pi}\int^\pi_{-\pi}f(x)\cos nxdx,(n=0,1,2,3,\cdots) \]
\[b_n=\frac{1}{\pi}\int^\pi_{-\pi}f(x)\sin nxdx,(n=1,2,3,\cdots) \]
定理 设\(f(x)\)是周期为\(2\pi\)的周期函数,如果它满足:
- 在一个周期内连续或只有有限个第一类间断点
- 在一个周期内至多只有有限个极值点
那么\(f(x)\)的傅立叶级数收敛,并且
当\(x\)是\(f(x)\)的连续点时,级数收敛于\(f(x)\);
当\(x\)是\(f(x)\)的间断点时,级数收敛于\(\frac{1}{2}[f(x^-)+f(x^+)]\)
如果函数只在\([-\pi,\pi]\)上有定义,可以使用周期延拓来展开成傅里叶级数。
正弦级数和余弦级数
当\(f(x)\)为奇函数时,可以展开为正弦级数
\[\sum_{n=1}^\infty b_n\sin nx \]
当\(f(x)\)为偶函数时,可以展开为余弦函数
\[\frac{a_0}{2}+\sum_{n=1}^\infty a_n\cos nx \]
一般周期的傅里叶级数
周期为\(2l\)
\[f(x)=\frac{a_0}{2}+\sum^\infty_{n=1}\left(a_ncos\frac{n\pi x}{l}+b_nsin\frac{n\pi x}{l}\right)(x\in C) \]
其中
\[a_n=\frac{1}{l}\int_{-l}^lf(x)cos\frac{n\pi x}{l}dx\quad (n=0,1,2,\cdots) \]
\[b_n=\frac{1}{l}\int_{-l}^lf(x)sin\frac{n\pi x}{l}dx\quad (n=1,2,3,\cdots) \]
\[C=\left\{x\left|f(x)=\frac{1}{2}[f(x^-) +f(x^+)]\right. \right\} \]