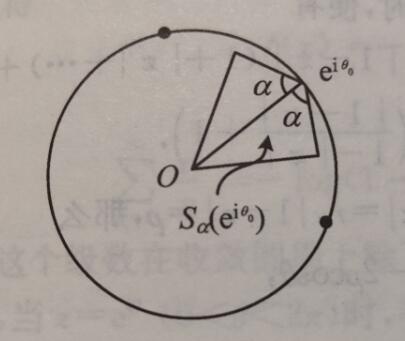复数与复变函数

复数的定义及其运算

把负数定义为一堆有序的实数\((a,b)\)，如果用\(\bm R\)作为实数集，\(\bm C\)为复数集，则

\[\bm C = \{(a,b):a\in\bm R,b\in\bm R\} \]

定义加法和乘法如下

\[(a,b)+(c,d)=(a+c,b+d) \]

\[(a,b)(c,d)=(ac-bd,ad+bc) \]

易知，加法和乘法满足交换率和结合律。

\((0,0)\)是零元素，\((-a,-b)\)是\((a,b)\)的负元素，\((1,0)\)是乘法的单位元素。每个非零元素\((a,b)\)的逆元素是\((\frac{a}{a^2+b^2},-\frac{b}{a^2+b^2})\)

此外还满足分配律

\[[(a,b)+(c,d)](e,f) = (a,b)(e,f)+(c,d)(e,f) \]

可以直接记\((a,0)=a\)。

对于\((0,1)\)有

\[(0,1)^2=(-1,0)=-1 \]

记为\((0,1)=i\)

同样有\((0,b)=(b,0)(0,1)=bi\)

于是每一个复数都可以写成

\[(a,b)=(a,0)+(0,b)=a+bi \]

定理1

复数域不是有序域，换句话说，不可以比较大小。

出于方便和其他一些原因，用\(z=a+bi\)来描述复数，\(a\)称为\(z\)的实部，\(b\)称为\(z\)的虚部。可以记为\(a=Rez,b=Imz\)。

四则运算

加法

\[(a+bi)+(c+di)=(a+c)+(b+d)i \]

乘法

\[(a+bi)(c+di)=(ac-bd)+(ad+bc)i \]

减法

\[(a+bi)-(c+di)=(a-c)+(b-d)i \]

除法

\[\frac{a+bi}{c+di}=(a+bi)\left(\frac{c-di}{c^2+d^2}\right)=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i \]

模

\[|z|=\sqrt{a^2+b^2} \]

共轭

\[\overline{z}=a-bi \]

定理2

\(Rez=(z+\overline{z})/2,Imz=(z-\overline z)/2i\)
\(z\overline z=|z|^2\)
\(\overline{z+w}=\overline z+\overline w,\overline{zw}=\overline z\cdot\overline w,\overline{z/w}=\overline{z}/\overline{w}\)
\(|zw|=|z||w|,|z/w|=|z|/|w|\)
\(|z|=|\overline z|\)
\(|Rez|\leq |z|,|Imz|\leq|z|\)
\(|z+w|\leq|z|+|w|\)当且仅当存在一个\(t\geq 0,z=tw\)时取等。
\(|z-w|\geq||z|-|w||\)

复数的几何表示

三角表示法

复数能用上一节提到的实数对\((a,b)\)表示，同时就可以看成平面上的一个点。同样的，也可以用极坐标\((r,\theta)\)表示，那么有，

\[a=rcos\theta,b=rsin\theta \]

所以复数也可以表示为

\[z=r(cos\theta+isin\theta) \]

其中\(r=|z|\)，\(\theta\)称为辐角，记为\(\theta=Argz\)。显然若\(\theta\)是辐角，那么\(\theta+2k\pi\)也是辐角。但在\(Argz\)中，只有一个辐角满足\(-\pi<\theta\leq\pi\)，称为辐角的主值，记为\(argz\)，所以有

\[Argz=argz+2k\pi,\quad k\in Z \]

特别注意，模为0的复数的辐角没有意义。

指数表示法

由欧拉公式

\[e^{i\theta}=cos\theta+isin\theta \]

得到

\[z=re^{i\theta} \]

de Moivre公式

设\(z_1=r_1(cos\theta_1+isin\theta_1),\cdots,z_n=r_n(cos\theta_n+isin\theta_n)\)是给定的n个复数，数学归纳法可知

\[z_1\cdots z_n=r_1\cdots r_n[cos(\theta_1+\cdots+\theta_n)+isin(\theta_1+\cdots+\theta_n)] \]

作为特殊情况，有

\[z^n=r^n(\cos n\theta+i\sin n\theta) \]

同样对于负整数也是成立的

\[z^{-n}=r^{-n}(\cos(-n\theta)+i\sin(-n\theta)) \]

现在设\(\omega=r(\cos\theta+i\sin\theta)\)是给定的，要求的\(z=\rho(\cos\varphi+i\sin\varphi)\).由de Moivre公式，\(z^n=\omega\)等价为

\[\rho^n(\cos n\varphi+i\sin n\varphi)=r(\cos\theta+i\sin\theta) \]

所以\(\rho=\sqrt[n]{r},n\varphi=\theta+2k\pi,k=0,1,\cdots,n-1\).共有\(n\)个复数满足\(z^n=w\)，即

\[z=\sqrt[n]{|\omega |}\left(\cos\frac{\theta+2k\pi}{n}+i\sin\frac{\theta+2k\pi}{n}\right),k=0,1,\cdots,n-1 \]

这\(n\)个复数恰好是以原点为中心，\(\sqrt[n]{|\omega |}\)为半径的圆的内接正\(n\)边形的顶点。

\(\omega=1\)时，若记\(w=\cos\frac{2\pi}{n}+i\sin\frac{2\pi}{n}\)，则\(\sqrt[n]{1}\)的\(n\)个值为

\[1,w,w^2,\cdots,w^{n-1} \]

称为\(n\)个单位根，如果用\(\sqrt[n]{\omega}\)的任一\(n\)次根，那么\(\omega\)的\(n\)个\(n\)次根又可以表示为

\[\sqrt[n]{\omega}, \sqrt[n]{\omega}w,\cdots,\sqrt[n]{\omega}w^{n-1} \]

扩充平面和复数的球面表示

因为需要，在\(\bm C\)中引入一个新的数\(\infty\)，其模是\(\infty\)，辐角没有意义，运算规则如下

\[z\pm\infty = \infty, z\cdot \infty = \infty(z\neq 0) \]

\[\frac{z}{\infty} = 0, \frac{z}{0} = \infty(z\neq 0) \]

而\(0\cdot \infty\)和\(\infty\pm\infty\)不规定意义。引入之后的复数系记为\(\bm C_\infty\)。在复平面上，没有一个点和\(\infty\)对应，但是我们想象有一个无穷远点和\(\infty\)对应，加上无穷远点的复平面称为扩充平面或闭平面。否则是开平面。

在复平面上，无穷远点和普通点是不一样的。但在黎曼引入的球面表示中没有什么区别。

设\(S\)是\(\bm R^3\)中的单位球面，即

\[S = \{(x_1,x_2,x_3)\in \bm R^3:x_1^2+x_2^2+x_3^2=1\} \]

把\(\bm C\)等同于平面

\[\bm C = \{(x_1,x_2,0):x_1,x_2\in \bm R\} \]

称\(N=(0,0,1)\)为北极点。在\(\bm C\)上的任一一点\(z\)，连接\(N,z\)的直线必然和\(S\)交于一点\(P\)。若\(|z|>1\)，则\(P\)在北半球；若\(|z|<1\)，则\(P\)在南半球；若\(|z|=1\)，则\(z\)就是\(P\)。

当\(z\)趋向\(\infty\)时，球面上的点就会趋向于\(N\)，所以就可以把\(\infty\)对应于\(N\)。这样一来\(\bm C_\infty\)中的所有点都可以被移植到球面上去了，并且所有的点一视同仁。

设\(z=x+iy\)，则\(P\)的坐标为

\[x_1=\frac{2x}{x^2+y^2+1},x_2=\frac{2y}{x^2+y^2+1},x_3=\frac{x^2+y^2-1}{x^2+y^2+1} \]

或者用复数表示为

\[x_1=\frac{z+\bar z}{1+|z|^2},x_2=\frac{z-\bar z}{i(1+|z|^2)},x_3=\frac{|z|^2-1}{|z|^2+1} \]

同样也就可以用球面上的点来表示复数

\[z=\frac{x_1+ix_2}{1-x_3} \]

复数列的极限

极限

复数列\(\{z_n\}\)收敛到点\(z_0\)，指的是对于任给的\(\varepsilon>0\)，存在正整数\(N\)，当\(n>N\)时，\(|z_n-z_0|<\varepsilon\)，记作\(\lim_{n\to \infty}z_n=z_0\)

复数列\(\{z_n\}\)收敛到\(\infty\)，指的是对于任意正数\(M>0\)，存在正整数\(N\)，当\(n>N\)时，\(|z_n|>M\)，记为\(\lim_{n\to\infty}z_n=\infty\)

邻域

对于\(a\in\bm C,r>0\)，称

\[B(a,r)=\{z\in C:|z-a|< r\} \]

为以\(a\)为中心、以\(r\)为半径的圆盘，特别当\(a=0,r=1\)时称为单位圆盘。\(B(a,r)\)也称为\(a\)点的一个\(r\)邻域，或简称邻域。无穷远点的邻域是指集合\(\{z\in \bm C:|z|>R\}\)，记为\(B(\infty, R)\)

此时极限有可以表示为：

\(\lim_{n\to \infty}z_n=z_0\)可以说成对任意\(\varepsilon>0\)，当\(n\)充分大时，\(z_n\in B(z_0,\varepsilon)\)

\(\lim_{n\to\infty}z_n=\infty\)可以说成对任意\(M>0\)，当\(n\)充分大时，\(z_n\in B(\infty, M)\)

同时马上就可以得到，\(\lim_{n\to \infty}z_n=z_0\)的充要条件是，其实部和虚部分别有\(\lim_{n\to \infty}x_n=x_0\)和\(\lim_{n\to \infty}y_n=y_0\)。

开集、闭集和紧集

内点

如果存在\(r>0\)，使得\(B(a,r)\subset E\)，就称\(a\)为\(E\)的内点

外点

如果存在\(r>0\)使得\(B(a,r)\subset E^c\)，就称\(a\)为\(E\)的外点。其中\(E^c\)是补集。

边界点

如果对于任意\(r>0\)，\(B(a,r)\)中既有\(E\)的点，也有\(E^c\)的点，就称\(a\)为\(E\)的边界点。

内部

\(E\)的内点的全体称为\(E\)的内部，记为\(E\degree\)

外部

\(E\)的外点的全体称为\(E\)的外部，记为\((E^c)\degree\)

边界

\(E\)的边界点的全体称为\(E\)的边界，记为\(\partial E\)

开集

如果\(E\)的所有点都是他的内点，即\(E=E\degree\)，就称\(E\)是开集。

另外，空集是开集。

闭集

如果\(E^c\)是开集，就称\(E\)为闭集。

另外，无限集是闭集。

极限点、聚点

如果对任意\(r>0\)，\(B(a,r)\)中除\(a\)外总有\(E\)中的点，则称\(a\)为极限点或聚点。

导集

集\(E\)的所有极限点构成的集称为\(E\)的导集，记为\(E'\)。

孤立点

\(E\)中不属于\(E'\)的点称为孤立点。

闭包

\(E\)和它的导集的并称为\(E\)的闭包，记为\(\bar E=E\cup E'\)

直径

点集\(E\)的直径定义为\(E\)中任意两点间距离的上确界，记为\(diamE\)，即

\[diamE=sup\{|z_1-z_2|:z_1,z_2\in E\} \]

Cantor定理

若非空闭集序列\(\{F_n\}\)满足

\(F_1\supset F_2\supset\cdots\supset F_n\supset\cdots\)
\(diamF_n\to 0\)（当\(n\to \infty\)时）

那么\(\bigcap^\infty_{n=1}F_n\)是一个独点集（只有一个点的集）。

开集族、开覆盖

设\(E\)是一个集，\(\mathscr{F}=\{G\}\)是一个开集族，即\(\mathscr{F}\)中的每一个元素都是开集。如果\(E\)中每一点至少属于\(\mathscr{F}\)中的一个开集，就说\(\mathscr{F}\)是\(E\)的一个开覆盖。

有限覆盖性质

点集\(E\)具有有限覆盖性质，是指从\(E\)的任一个开覆盖中必能选出有限个开集\(G_1,\cdots,G_n\)，使得这有限个开集的并就能覆盖\(E\)，即

\[E\subset\bigcup^n_{j=1}G_j \]

紧集

具有有限覆盖性质的集称为紧集。

有界

集\(E\)称为是有界的，如果存在\(R>0\)，使得\(E\subset B(0,R)\)

Heine-Borel定理

在\(C\)中，\(E\)是紧集的充要条件为\(E\)是有界闭集；在\(C_\infty\)中，\(E\)是紧集的充要条件为\(E\)是闭集。

定理

设\(E\)是紧集，\(F\)是闭集，且\(E\cap F=\empty\)，则

\[d(E,F) > 0 \]

其中

\[d(E,F) = \inf\{|z_1-z_2|:z_1\in E, z_2\in F\} \]

Bolzano-Weierstrass定理

任一无穷点集至少有一个极限点。

曲线和域

连续曲线

定义在闭区间\([a,b]\)上的一个复值连续函数\(\gamma:[a,b]\to \bm C\)，写为

\[z = \gamma(t)=x(t)+iy(t),\quad a\leq t\leq b \]

这里\(x(t),y(t)\)都是\([a,b]\)上的连续函数。

如果用\(\gamma^*\)记\(\gamma\)的像点所成的集合

\[\gamma^* = \{\gamma(t):a\leq t\leq b\} \]

那么\(\gamma^*\)是\(\bm C\)上的紧集。

曲线\(\gamma\)的方向就是\(t\)增加的方向。此时\(\gamma(a)\)为起点，\(\gamma(b)\)为终点。

闭曲线

如果\(\gamma(a)=\gamma(b)\)，则称为闭曲线。

简单曲线

如果当且仅当\(t_1=t_2\)时才有\(\gamma(t_1)=\gamma(t_2)\)，则称为简单曲线或Jordan曲线。

简单闭曲线

如果当且仅当如果当且仅当\(t_1=a,t_2=b\)时才有\(\gamma(t_1)=\gamma(t_2)\)，则称为简单闭曲线或Jordan闭曲线，或简称围道。

可求长的

设\(z=\gamma(t)\)是一条曲线，对区间\([a,b]\)做分割\(a=t_0< t_1<\cdots< t_n=b\)，得到以\(z_k=\gamma(t_k)\)为顶点的折线\(P\)，那么\(P\)的长度为

\[|P|=\sum_{k=1}^n|\gamma(t_k)-\gamma(t_{k-1})| \]

如果不论如何分割区间\([a,b]\)，所得折线的长度都是有界的，就称曲线\(\gamma\)是可求长的，其长度定义为\(\gamma\)的上确界。

光滑曲线

如果\(\gamma'(t)=x'(t)+iy'(t)\)存在，且\(y'(t)\neq 0\)，那么\(\gamma\)在每一点都有切线，\(\gamma'(t)\)就是曲线\(\gamma\)在\(\gamma(t)\)处的切向量，它与正实轴的夹角为\(Arg\gamma'(t)\)，

如果\(\gamma'(t)\)是连续函数，那么\(\gamma\)的切线随\(t\)而连续变动，这时称\(\gamma\)为光滑曲线。

此时\(\gamma\)的长度为

\[\int^b_a \sqrt{(x'(t))^2+(y'(t))^2}dt = \int^b_a|\gamma'(t)|dt \]

曲线\(\gamma\)称为逐段光滑的。

如果存在\(t_0,t_1,\cdots,t_n\)，使得\(a=t_0< t_1<\cdots< t_n=b\)，\(\gamma\)在每个参数区间\([t_{j-1},t_j]\)上是光滑的，那么在每个分点\(t_1,\cdots,t_{n-1}\)处\(\gamma\)的左右导数存在。

连通性

平面点集\(E\)称为是联通的，如果对任意两个不相交的非空集\(E_1\)和\(E_2\)满足

\[E = E_1\bigcup E_2 \]

那么\(E_1\)必含有\(E_2\)的极限点，或者\(E_2\)必含有\(E_1\)的极限点，也就是说，\(E_1\cap\bar E_2\)和\(E_2\cap\bar E_1\)至少有一个非空。

定理1

平面上的非空开集\(E\)是连通的充分必要条件是：\(E\)中任意两点可用位于\(E\)中的折线连接起来。

域

非空的连通开集称为域

Jordan定理

一条简单闭曲线\(\gamma\)吧复平面分成两个域，其中一个是有界的，称为\(\gamma\)的内部；另一个是无界的，称为\(\gamma\)的外部，而\(\gamma\)是这两个域的共同的边界。

单连通与多连通

域\(D\)称为是单连通的，如果\(D\)内任意简单闭曲线的内部仍在\(D\)内。

不是单连通的域称为多连通的。

如果域\(D\)是由\(n\)跳简单闭曲线围成的，就称\(D\)是\(n\)连通的，简单闭曲线中也可以有退化成一条简单曲线或一点的。

复变函数的极限和连续性

设\(E\)是复平面上一点集，如果对每一个\(z\in E\)，按照某一规则有一确定复数\(\omega\)与之对应，我们就说在\(E\)上确定了一个单值复变函数，记为\(\omega=f(z)\)或\(f:E\to C\)。

\(E\)称为\(f\)的定义域，点集\(\{f(z):z\in E\}\)称为\(f\)的值域。

如果对于\(z\in E\)，对应的\(\omega\)有几个或无穷多个，则称在\(E\)上确定了一个多值函数。

复变函数是定义在平面点集上的，而它的值域也是一个平面点集，因此复变函数也称为映射，它把一个平面点集映成另一个平面点集。

设\(z=x+iy\)，用\(u\)和\(v\)记\(\omega=f(z)\)的实部和虚部，则有

\[\omega=f(z)=u(z)+iv(z)=u(x,y)+iv(x,y) \]

这就是说，一个复变函数等价于两个二元的实变函数。

极限

设\(f\)是定义在点集\(E\)上的一个复变函数，\(z_0\)是\(E\)的一个极限点，\(a\)是给定的一个复数。如果对任意的\(\varepsilon>0\)，存在于\(\varepsilon\)有关的\(\delta>0\)，使得当\(z\in E\)且\(0<|z-z_0|<\delta\)时有\(|f(z)-a|<\varepsilon\)，就说当\(z\to z_0\)时\(f(z)\)有极限\(a\)，记作\(\lim_{z\to z_0}f(z)=a\)。

\(\lim_{z\to z_0}f(z)=a\)的充分必要条件是

\[\lim_{x\to x_0,y\to y_0}u(x,y)=\alpha,\lim_{x\to x_0,y\to y_0}v(x,y)=\beta \]

连续

我们说\(f\)在点\(z_0\in E\)连续，如果

\[\lim_{z\to z_0}f(z)=f(z_0) \]

如果\(f\)在集\(E\)中每点都连续，就说\(f\)在集\(E\)上连续。

定理

设\(E\)是\(\bm C\)中的紧集，\(f:E\to\bm C\)在\(E\)上连续，那么

\(f\)在\(E\)上有界
\(|f|\)在\(E\)上能取得最大值和最小值，即存在\(a,b\in E\)使得对于每个\(z\in E\)都有

\[|f(z)|\leq |f(a)|，|f(z)|\geq|f(b)| \]

\(f\)在\(E\)上一致连续。即对任意\(\varepsilon>0\)，存在只与\(\varepsilon\)有关的\(\delta>0\)，对\(E\)上任意的\(z_1,z_2\)，只要\(|z_1-z_2|<\delta\)，就有\(|f(z_1)-f(z_2)|<\varepsilon\)

全纯函数/解析函数

复变函数的导数

设\(f:D\to\bm C\)是定义在域\(D\)上的函数，\(z_0\in D\)，如果极限

\[\lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0} \]

存在，就说\(f\)在\(z_0\)处复可导或可微，这个极限称为在此处的导数或微商。

如果\(f\)在\(D\)中每点都可微，就称\(f\)是域\(D\)中的全纯函数或解析函数。

如果\(f\)在\(z_0\)的一个邻域中全纯，就称\(f\)在\(z_0\)处全纯。

定理1

如果\(f\)在\(z_0\)处可微，则必在\(z_0\)处连续。反过来说则不一定成立。

求复变函数的导数时，跟一元实变函数几乎没有什么区别，例如\(f(z)=z^3, f'(z)=3z^2\)。但是更加严格的一点时，在复平面上任何一个方向上的导数都要相等，而不是一元实变函数左右相等。

实变函数的四则运算的求导法则在全纯函数中也成立。

定理2

设\(D_1,D_2\)是\(\bm C\)中的两个域，且

\[f:D_1\to D_2\\ g:D_2\to\bm C \]

都是全纯函数，那么\(h=g\circ f\)是\(D_1\to \bm C\)的全纯函数，并且\(h'(z)=g'(f(z))f'(z)\)

Cauchy-Riemann方程

实可微

设\(f(z)=u(x,y)+iv(x,y)\)是定义在域\(D\)上的函数，\(z_0=x_0+iy_0\in D\).我们说\(f\)在\(z_0\)处实可微，是指\(u,v\)作为\(x,y\)的二元函数在\((x_0,y_0)\)处可微。

设\(f:D\to C\)是定义在域\(D\)上的函数，\(z_0\in D\)，那么\(f\)在\(z_0\)处实可微的充要条件是下式成立

\[f(z_0+\Delta z)-f(z_0)=\frac{\partial f}{\partial z}(z_0)\Delta z+\frac{\partial f}{\partial \bar z}(z_0)\Delta z+o(|\Delta z|) \]

其中算子定义如下

\[\frac{\partial}{\partial z}=\frac{1}{2}\left(\frac{\partial}{\partial x}-i\frac{\partial}{\partial y}\right) \]

\[\frac{\partial}{\partial \bar z}=\frac{1}{2}\left(\frac{\partial}{\partial x}+i\frac{\partial}{\partial y}\right) \]

在进行微分运算时，可以把\(z,\bar z\)看成独立的变量。

柯西-黎曼方程

设\(f\)是定义在域\(D\)上的函数，\(z_0\in D\)，那么\(f\)在\(z_0\)处可微的充要条件是\(f\)在\(z_0\)处实可微且\(\frac{\partial f}{\partial \bar z}(z_0)=0\).

在可微的情况下，\(f'(z_0)=\frac{\partial f}{\partial z}(z_0)\).

其中\(\frac{\partial f}{\partial \bar z}(z_0)=0\)就称为柯西-黎曼方程。

将\(u,v\)代入以及算子展开，可以得到其等价于

\[\left\{\begin{matrix} \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x} \end{matrix}\right. \]

设\(D\)是\(\bm C\)中的域，用\(C(D)\)表示\(D\)上连续函数的全体，\(H(D)\)表示\(D\)上全纯函数的全体。

用\(C^1(D)\)记\(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\)在\(D\)上连续的\(f\)的全体。

\(C^k(D)\)记在\(D\)上有\(k\)阶连续偏导数的函数的全体，\(C^\infty(D)\)记在\(D\)上有任意阶连续偏导数的函数的全体。

之后我们用柯西积分公式证明，有

\[H(D)\subset C^\infty(D)\subset C^k(D)\subset C^1(D)\subset C(D) \]

即域\(D\)上的全纯函数在\(D\)上有任意阶的连续偏导数。

调和函数

设\(u\)是域\(D\)上的实值函数（或称二元实变函数），如果\(u\in C^2(D)\)，且对于任意\(z\in D\)，有

\[\Delta u(z)=\frac{\partial^2u(z)}{\partial x^2}+\frac{\partial^2u(z)}{\partial y^2}=0 \]

就称\(u\)是\(D\)中的调和函数。

\[\Delta=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2} \]

称为拉普拉斯算子。

定理1

设\(f=u+iv\in H(D)\)，那么\(u,v\)都是\(D\)上的调和函数。

共轭调和函数

设\(u,v\)是\(D\)上的一对调和函数，如果它们还满足柯西-黎曼方程，

\[\left\{\begin{matrix} \frac{\partial u}{\partial x}=\frac{\partial v}{\partial y} \\ \frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x} \end{matrix}\right. \]

就称\(v\)为\(u\)的共轭调和函数。

定理1

设\(u\)是单连通域\(D\)上的调和函数，则必存在\(u\)的共轭函数\(v\)，使得\(u+iv\)是\(D\)上的全纯函数。

其中

\[v(x,y) = \int^{(x,y)}_{(x_0,y_0)}\dfrac{\partial v}{\partial x}dx+\dfrac{\partial v}{\partial y}dy = \int^{(x,y)}_{(x_0,y_0)}-\dfrac{\partial u}{\partial y}dx+\dfrac{\partial u}{\partial x}dy \]

且这个积分与路径无关。

反过来说如果有\(v\)，则也必存在\(u\)

\[u(x,y) = \int^{(x,y)}_{(x_0,y_0)}\dfrac{\partial u}{\partial x}dx+\dfrac{\partial u}{\partial y}dy = \int^{(x,y)}_{(x_0,y_0)}\dfrac{\partial v}{\partial y}dx-\dfrac{\partial v}{\partial x}dy \]

导数的几何意义

过\(z_0\)点作一条光滑曲线\(\gamma\)，它的方程为

\[z = \gamma(t),a\leq t\leq b \]

设\(\gamma(a)=z_0,\gamma'(a)\neq 0\)。\(\gamma\)在点\(z_0\)处的切线与正实轴的夹角为\(Arg\gamma'(a)\)。设\(\omega = f(z)\)把曲线\(\gamma\)映为\(\sigma\)，它的方程为

\[\omega=\sigma(t)=f(\gamma(t)),a\leq t\leq b \]

由于\(\sigma'(a)=f'(\gamma(a))\gamma'(a)=f'(z_0)\gamma'(a)\neq 0\)，所以\(\sigma\)在\(\omega_0=f(z_0)\)处的切线与正实轴的夹角为

\[Arg\sigma'(a) = Argf'(z_0)+Arg\gamma'(a) \]

或者写为

\[Arg\sigma'(a) - Arg\gamma'(a) = Argf'(z_0) \]

这就说明像曲线\(\sigma\)在\(\omega_0\)处的切线与正实轴的夹角与原曲线\(\gamma\)在\(z_0\)处的切线与正实轴的夹角之差总是\(Argf'(z_0)\)，而与曲线\(\gamma\)无关，\(Argf'(z_0)\)就称为映射\(\omega=f(z)\)在\(z_0\)处的转动角。

过点\(z_0\)作两条光滑曲线\(\gamma_1,\gamma_2\)，它们的方程分别为

\[z=\gamma_1(t),a\leq t\leq b \]

和

\[z=\gamma_2(t),a\leq t\leq b \]

且\(\gamma_1(a)=\gamma_2(a)=z_0\)。映射\(\omega=f(z)\)把它们分别映为过\(\omega_0\)点的两条光滑曲线\(\sigma_1\)和\(\sigma_2\)，他们的方程分别为

\[\omega = \sigma_1(t)=f(\gamma_1(t)),a\leq t\leq b \]

\[\omega = \sigma_2(t)=f(\gamma_2(t)),a\leq t\leq b \]

因为\(\sigma'(a)=f'(\gamma(a))\gamma'(a)=f'(z_0)\gamma'(a)\neq 0\)，所以有

\[Arg\sigma'(a) = Argf'(z_0)+Arg\gamma'(a) \]

或者写为

\[Arg\sigma'(a)-Arg\gamma'(a) = Argf'(z_0) \]

由此就有

\[Arg\sigma_1'(a)-Arg\gamma_1'(a) = Argf'(z_0) = Arg\sigma_2'(a)-Arg\gamma_2'(a) \]

上式说明，如果\(f'(z_0)\neq 0\)，那么在映射\(\omega=f(z)\)的作用下，过\(z_0\)点的任意两条光滑曲线的夹角的大小与旋转方向都是保持不变的。

我们把这种性质的映射称为在\(z_0\)点是保角的。

定理

全纯函数在其导数不为零的点处是保角的。

导数的模的几何意义

\(|f'(z_0)|\)为\(f\)在\(z_0\)处的伸缩率。

像点之间的距离与原像之间的距离之比只与\(z_0\)有关，而与\(\gamma\)无关。

共形映射的概念

综合导数辐角和模的几何意义，我们看到：如果\(f'(z_0)\neq0\)，在\(z_0\)的邻域中，作一个以\(z_0\)为顶点的小三角形，这个小三角形被\(f\)映射为一个曲边三角形，它的微分三角形和原来的小三角形相似。因此，我们把这样的一个映射称为共形映射。

更形式化的定义是：设函数\(\omega=f(z)\)在\(z_0\)的领域内有定义，且在\(z_0\)处具有保角性和伸缩率的不变性，那么称映射\(\omega=f(z)\)是共形映射。如果对\(D\)内每一点都是共形的，那么\(\omega=f(z)\)是在\(D\)内的共形映射。

如果\(\omega=f(z)\)在\(z_0\)全纯，\(f'(z_0)\neq 0\)，那么其在\(z_0\)是共形的。

如果\(\omega=f(z)\)只保证伸缩率的不变性和夹角的绝对值不变（但方向相反），那么称为第二类共形映射，之前提到的属于第一类共形映射。

初等全纯函数

指数函数

设\(z=x+iy\)，定义

\[e^z = e^x(\cos y+i\sin y) \]

具有如下性质

\((e^z)'=e^z\)
复数的三角表示\(z=r(\cos\theta+i\sin\theta)\)可以表示为\(z=re^{i\theta}\)
对于任意\(z\in \bm C,e^z\neq 0\)，这是因为

\[|e^z|=e^x>0 \]

对于任意\(z_1,z_2\)，有

\[e^{z_1}e^{z_2}=e^{z_1+z_2} \]

\(e^z\)是以\(2\pi i\)为周期的周期函数。

单叶

设\(f:D\to \bm C\)是一个复变函数，如果对于\(D\)中的任意两点\(z_1,z_2(z_1\neq z_2)\)，必有\(f(z_1)\neq f(z_2)\)，就称\(f\)在\(D\)中是单叶的，\(D\)称为\(f\)的单叶性域。

\(\omega=e^z\)的单叶性域有

\[\{z=x+iy:2k\pi< y<2(k+1)\pi\},k=0,\pm1,\cdots \]

对数函数

对于给定的\(z\in C\)，满足方程\(e^\omega=z\)的\(\omega\)称为\(z\)的对数，记为\(\omega=Logz\)。

设\(z=re^{i\theta}\)，\(\omega=u+iv\)，则\(e^{u+iv}=re^{i\theta}\)，所以\(e^u=r,v=\theta+2k\pi\)。所以有

\[Logz=log|z|+iargz+2k\pi i=log|z|+iArgz \]

所以，\(Logz\)是一个多值函数，它的多值性是由\(z\)的辐角\(Argz\)的多值性产生的。

定理1

如果\(D\)是不包含原点和无穷远点的单连通域，则必在\(D\)上存在无穷多个单值全纯函数\(\varphi_k,k=0,\pm1,\cdots\)，使得在\(D\)上成立

\[e^{\varphi_k(z)}=z,k=0,\pm1,\cdots; \]

而且对每一个\(k\)，有\(\varphi_k'(z)=\frac{1}{z}\).其中的每一个\(\varphi_k\)都称为\(Logz\)在\(D\)上的单值全纯分支。

至于为什么不包含原点和无穷远点：如果包含原点，那么\(D\)中就包含绕原点\(z=0\)的简单闭曲线\(\gamma\)，当\(z\)从\(\gamma\)上的一点\(z_0\)沿\(\gamma\)的正方向（即逆时针）回到\(z_0\)时，\(z\)的辐角增加了\(2\pi\)，\(\varphi_{k_0}(z_0)\)的值连续地变为\(\varphi_{k_0+1}(z_0)\)，而不再回到原来的\(\varphi_{k_0}(z_0)\)。因此再这样的域中就不可能分出单值的全纯分支。无穷远点同理。

定义1

如果当\(z\)沿着\(z_0\)的充分小邻域中的任意简单闭曲线绕一圈时，多值函数的值就从一支变到另一支，那么称\(z_0\)为该多值函数的一个支点。

以对数函数为例，\(z=0,z=\infty\)就是\(Logz\)的支点。

幂函数

\(\omega=z^\mu\)称为幂函数，这里\(\mu=a+bi\)，分情况讨论

1. \(\mu=n\)，是一个自然数

按照导数的定义，可以直接算出

\[(z^n)'=nz^{n-1} \]

其在\(C\)上每一点都是全纯的。这种函数也称作整函数

它的单叶性域是

\[\bigg\{z:\alpha < argz<\beta,0<\beta-\alpha\leq\frac{2\pi}{n}\bigg\} \]

2. \(\mu=\frac{1}{n}\)，n是一个自然数

对于一个给定的\(z\)，\(z^{1/n}\)有\(n\)个值，所以它是一个多值函数。多值性由\(Argz\)产生，\(0,\infty\)是其支点。\(C\)去掉正实轴后所成的域上可以分出\(n\)个单值的全纯分支，它们是

\[\omega = \varphi_k(z) = \sqrt[n]{|z|}\bigg(\cos\frac{\theta+2k\pi}{n}+i\sin\frac{\theta+2k\pi}{n}\bigg) \]

\[k=0,1,\cdots,n-1 \]

其中\(\theta=argz\)，变化范围在\(0< argz<2\pi\)

3. \(\mu = a+bi\)，是一个复数

一般的幂函数\(\omega=z^\mu\)定义为

\[\omega = z^\mu=e^{\mu Logz} \]

显然这也是个多值函数

\[\omega = exp(alog|z|-b(argz+2k\pi))exp(i[blog|z|+a(argz+2k\pi)]) \]

\[k=0,\pm1,\cdots \]

若\(b=0,a=n\)是一个整数，则\(\omega=z^n\)是一个单值函数
若\(b=0,a=p/q\)是一个有理数，不妨设\(p< q\)，这时

\[\omega=z^\mu=z^{p/q}=|z|^{p/q}exp(i\frac{p}{q}(argz+2k\pi)) \]

当\(k=0,1,\cdots,q-1\)时，\(\omega\)有\(q\)个不同的值

若\(b=0,a\)是一个无理数，这时

\[\omega = z^\mu = |z|^aexp(iaargz)exp(i2k\pi a) \]

此时\(z^a\)是一个无穷值函数

若\(b\neq 0\)，则\(\omega=z^\mu\)是一无穷值函数。

三角函数

由欧拉公式知道

\[e^{ix} = \cos x+i\sin x\\ e^{-ix} = \cos x -i\sin x \]

可以得到

\[\cos z = \frac{1}{2}(e^{iz}+e^{-iz})\\ \sin z = \frac{1}{2i}(e^{iz}-e^{-iz}) \]

有如下性质

正弦余弦都是整函数，并且

\[(\cos z)' = -\sin z\\ (\sin z)' = \cos z \]

以\(2\pi\)为周期
\(\cos z\)是偶函数，\(\sin z\)是奇函数
对任意\(z_1,z_2\)

\[\cos (z_1+z_2) = \cos z_1\cos z_2 - \sin z_1\sin z_2\\ \sin (z_1+z_2) = \sin z_1\cos z_2 + \cos z_1\sin z_2\\ \]

\(\cos^2 z+\sin^2 z=1,\quad \sin 2z = 2\sin z\cos z\)
\(\sin z\)仅在\(z=k\pi\)处为零，\(\cos z\)仅在\(k\pi+\pi/2\)处为零，\(k=0,\pm1,\cdots\)
\(\cos z,\sin z\)不是有界函数

同样我们就能定义正切余切

\[\tg z = \frac{\sin z}{\cos z} \]

\[\ctg z = \frac{\cos z}{\sin z} \]

前者在除掉\(z=\pi/2+k\pi\)的开平面上全纯，后者在除掉\(z=k\pi\)的开平面上全纯，\(k=0,\pm1,\cdots\)。

之后我们也能定义双曲函数

\[chz=\frac{e^z+e^{-z}}{2},shz=\frac{e^z-e^{-z}}{2} \]

并且有

\[(chz)'=shz,(shz)'=chz \]

反三角函数有

\[Arcsinz=-iLn(iz+\sqrt{1-z^2}) \]

\[Arccosz=-iLn(z+\sqrt{z^2-1}) \]

\[Arctanz=-\frac{i}{2}Ln\frac{1+iz}{1-iz} \]

反双曲函数有

\[Arshz = Ln(z+\sqrt{z^2+1}) \]

\[Archz = Ln(z+\sqrt{z^2-1}) \]

\[Arthz = \frac{1}{2}Ln\frac{1+z}{1-z} \]

分式线性变换

形如\(\omega=T(z)=\frac{az+b}{cz+d}\)的映射称为分式线性变换或Mobius变换，其中\(a,b,c,d\)是复常数，且满足\(ad-bc\neq 0\)，如果等于\(0\)原式就是常数或无意义，没有讨论价值。

如果\(c\neq 0\)，则除去点\(z=-\frac{d}{c}\)外，\(T(z)\)在\(\bm C\)上是全纯的，而且

\[T'(z)=\frac{ad-bc}{(cz+d)^2}\neq 0 \]

所以分式线性变换在\(z\neq -\frac{d}{c}\)处是保角变换。

若\(c=0\)，则必\(d\neq 0\)，此时\(T(z)=Az+B(A=a/d,B=b/d)\)，称为整线性变换，它是一个整函数。

从方程\(\omega=T(z)\)中把\(z\)解出来，得

\[z = T^{-1}(\omega)=\frac{-d\omega+b}{c\omega-a} \]

称为\(\omega=T(z)\)的逆变换，它仍然是一个分式线性变换。由此可知\(\omega=T(z)\)在\(\bm C\)上是单叶的，当\(c\neq 0\)时，规定\(T(-\frac{d}{c})=\infty,T(\infty)=\frac{a}{c}\)。当\(c=0\)时，规定\(T(\infty)=\infty\)，于是\(\omega=T(z)\)把\(\bm C_\infty\)单叶地映射为\(C_\infty\)。

设\(S,T\)是两个分式线性变换，那么\(S\circ T\)也是分式线性变换。且对每一个\(T\)，都有逆变换\(T^{-1}\)，即\(T(T^{-1}(z))=z\)

分式线性变换有如下性质

保角性
分式线性变换把圆周变成圆周（保圆性）

分式线性变换也能拆成多个变换，例如

\[\omega = \dfrac{az+b}{cz+d} \]

就可以拆成三个变换

\[z' = cz+d\\ z'' = \dfrac{1}{z'}\\ \omega=\alpha+\beta z'' \]

其中\(\alpha = \dfrac{a}{c},\beta=\dfrac{bc-ad}{c}\)。

这个变换中第一个第三个是整线性变换，也就是进行了伸缩和平移变换。当然圆在伸缩和平移后还是一个圆。我们同样可以证明\(\omega=\dfrac{1}{z}\)把圆周变为圆周，此时我们证明了分式线性变换把圆周变为圆周。

交比是分式线性变换的不变量

命题1

分式线性变换\(T\)最多只有两个不动点，除非是恒等变换，即\(T(z)\equiv z\)

定义1

设\(z_1,z_2,z_3,z_4\)是给定的四个点，其中至少有三个点是不相同的，称比值

\[\frac{z_1-z_3}{z_1-z_4}\bigg /\frac{z_2-z_3}{z_2-z_4} \]

为这四个点的交比，记为\((z_1,z_2,z_3,z_4)\)

规定

\[(\infty,z_2,z_3,z_4)=\frac{z_2-z_4}{z_2-z_3} \]

\[(z_1,\infty,z_3,z_4)=\frac{z_1-z_3}{z_1-z_4} \]

\[(z_1,z_2,\infty,z_4)=\frac{z_2-z_4}{z_1-z_4} \]

\[(z_1,z_2,z_3,\infty)=\frac{z_1-z_3}{z_2-z_3} \]

按照交比的定义，有

\[(z,z_2,z_3,z_4)=\frac{z-z_3}{z-z_4}\cdot\frac{z_2-z_4}{z_2-z_3} \]

它是一个分式线性变换，若把它记为\(L(z)\)，那么

\[L(z_2)=1,\\ L(z_3)=0,\\ L(z_4)=\infty. \]

定理1

有且只有一个分式线性变换把\(\bm C_\infty\)上三个不同的点\(z_2,z_3,z_4\)映为事先给定的\(\bm C_\infty\)上的三个点\(\omega_2,\omega_3,\omega_4\)

定理2

交比是分式线性变换的不变量。也就是说，如果分式线性变换\(T\)把\(z_1,z_2,z_3,z_4\)映为\(T(z_1),T(z_2),T(z_3),T(z_4)\)，那么

\[(z_1,z_2,z_3,z_4)=(T(z_1),T(z_2),T(z_3),T(z_4)) \]

定理3

如果\(f(z_1,z_2,z_3,z_4)\)是分式线性变换下的不变量，即对任意分式线性变换\(T\)都有

\[f(z_1,z_2,z_3,z_4) = f(T(z_1),T(z_2),T(z_3),T(z_4)) \]

那么\(f\)只能是交比\((z_1,z_2,z_3,z_4)\)的函数。

命题2

四点\(z_1,z_2,z_3,z_4\)共圆的充要条件是

\[Im(z_1,z_2,z_3,z_4)=0 \]

定义2

设\(\bm C_\infty\)上的圆周\(\gamma\)把平面分成\(g_1\)和\(g_2\)两个域，\(z_1,z_2,z_3\)是\(\gamma\)上有序的三个点。如果当我们从\(z_1\)走到\(z_2\)再走到\(z_3\)时，\(g_1\)和\(g_2\)分别在我们的左边和右边，就分别称\(g_1\)和\(g_2\)为\(\gamma\)关于走向\(z_1,z_2,z_3\)的左边和右边

命题3

\(z_1,z_2,z_3\)是\(\bm C_\infty\)上的圆周\(\gamma\)上有序的三个点，那么\(\gamma\)关于走向\(z_1,z_2,z_3\)的右边和左边的点\(z\)分别满足

\[Im(z,z_1,z_2,z_3)>0\\ Im(z,z_1,z_2,z_3)<0 \]

定理4

设\(\gamma_1\)和\(\gamma_2\)是\(\bm C_\infty\)中的两个圆周，\(z_1,z_2,z_3\)是\(\gamma_1\)上有序的三个点，如果分式线性变换\(T\)把\(\gamma_1\)映为\(\gamma_2\)，那么它一定把\(\gamma_1\)关于走向\(z_1,z_2,z_3\)的右边和左边分别变为\(\gamma_2\)关于走向\(T(z_1),T(z_2),T(z_3)\)的右边和左边。

对称点及其在分布线性变换下的不变性

定义1

设\(\gamma\)是以\(a\)为中心，以\(R\)为半径的圆周，如果点\(z,z^*\)在从\(a\)出发的射线上，且满足

\[|z-a||z^*-a|=R^2 \]

则称\(z,z^*\)是关于\(\gamma\)对称的。如果\(\gamma\)是直线时，则当\(\gamma\)是线段\([z,z^*]\)的垂直平分线时，称\(z,z^*\)关于\(\gamma\)是对称的。

其中

\[z^* = a+\dfrac{R^2}{\bar{z}-\bar{a}} \]

命题1

设\(\gamma\)是\(\bm C_\infty\)中的圆周，那么\(z,z^*\)关于\(\gamma\)对称的充要条件是对\(\gamma\)上任意三点\(z_1,z_2,z_3\)，有

\[(z^*,z_1,z_2,z_3)=\overline{(z,z_1,z_2,z_3)} \]

对于直线的情形，可以看做无限半径的圆。

定理1

对称点在分式线性变换下不变。这就是说，设分式线性变换\(T\)把圆周\(\gamma\)变为\(\Gamma\)，如果\(z,z^*\)是关于\(\gamma\)的对称点，那么\(T(z),T(z^*)\)是关于\(\Gamma\)的对称点。

全纯函数的积分表示

复变函数的积分

设\(z=\gamma(t)(a\leq t\leq b)\)是一条可求长曲线，\(f\)是定义在\(\gamma\)上的函数，沿\(\gamma\)的正方向取分点\(\gamma(a)=z_0,z_1,z_2,\cdots,z_n=\gamma(b)\)，在\(\gamma\)中从\(z_{k-1}\)到\(z_k\)的弧段上任取点\(\zeta_k,k=1,\cdots,n\)，作Riemann和

\[\sum_{k=1}^n f(\zeta_k)(z_k-z_{k-1}) \]

用\(s_k\)记弧段\(z_{k-1}z_k\)的长度，如果\(\lambda=max\{s_k\}\to 0\)时，不论\(\zeta_k\)的取法，上式总有一确定的极限，就称次极限为\(f\)沿\(\gamma\)的积分，记为

\[\int_{\gamma}f(z)dz = \lim_{\lambda\to 0}\sum_{k=1}^n f(\zeta_k)(z_k-z_{k-1}) \]

只要\(f\)在\(\gamma\)上连续，上述积分、上述极限一定存在。

命题1

设\(f=u+iv\)在可求长曲线\(\gamma\)上连续，则有

\[\int_{\gamma}f(z)dz = \int_{\gamma}udx-vdy+i\int_{\gamma}vdx+udy \]

或者便于记忆

\[f(z)dz = (u+iv)(dx+idy) = (udx-vdy)+i(vdx+udy) \]

如果曲线光滑，还可以通过曲线的参数方程来计算积分。

命题2

如果\(z=\gamma(t)(a\leq t\leq b)\)是光滑曲线，\(f\)在\(\gamma\)上连续，那么

\[\int_{\gamma}f(z)dz = \int^b_af(\gamma(t))\gamma'(t)dt \]

命题3

如果\(f,g\)在可求长曲线\(\gamma\)上连续，那么

\(\int_{\gamma^-}f(z)dz=-\int_{\gamma}f(z)dz\)，\(\gamma^-\)是与\(\gamma\)反向的曲线
\(\int_{\gamma}f(\alpha f(z)+\beta g(z))dz=\alpha\int_{\gamma}f(z)dz+\beta \int_{\gamma}g(z)dz\)，\(\alpha,\beta\)是两个复常数
\(\int_{\gamma}f(z)dz=\int_{\gamma_1}f(z)dz+\int_{\gamma_2}f(z)dz\)，这里\(\gamma\)是由\(\gamma_1\)和\(\gamma_2\)组成的曲线。

命题4

如果\(\gamma\)的长度为\(L\)，\(M=\sup|f(z)|\)（即上确界），那么

\[\bigg |\int_\gamma f(z)dz\bigg |\leq ML \]

Cauchy积分定理

Cauchy定理

设\(D\)是\(\bm C\)中的单连通域，\(f\in H(D)\)（即全纯函数），且\(f'\)在\(D\)中连续，则对\(D\)中任意的可求长闭曲线\(\gamma\)，均有

\[\int_\gamma f(z)dz = 0 \]

注意，只要使得\(f\)的不全纯的点在\(\gamma\)包围的区域中（而不是必须在\(\gamma\)上）就不能使用这个定理。

引理1

设\(f\)是域\(D\)中的连续函数，\(\gamma\)是\(D\)内的可求长曲线，对于任给的\(\varepsilon>0\)，一定存在一条\(D\)中的折线\(P\)，使得

\(P\)和\(\gamma\)有相同的起点和终点，\(P\)中其他的顶点都在\(\gamma\)上
\(|\int_\gamma f(z)dz-\int_P f(z)dz|<\varepsilon\)

Cauchy-Goursat定理

设\(D\)是\(\bm C\)中的单连通域，如果\(f\in H(D)\)，那么对\(D\)中任意的可求长闭曲线\(\gamma\)，均有

\[\int_\gamma f(z)dz = 0 \]

注意点同上。

这个定理也意味着积分和路径无关，只与始末位置有关。

定理1

设\(D\)是可求长简单闭曲线\(\gamma\)的内部，若\(f\in H(D)\bigcap C(\bar D)\)（即在\(D\)上全纯且在\(\bar D\)（闭包）上连续），则

\[\int_\gamma f(z)dz = 0 \]

定理2

设\(\gamma_0,\gamma_1,\cdots,\gamma_n\)是\(n+1\)条可求长简单闭曲线，\(\gamma_1,\cdots,\gamma_n\)都在\(\gamma_0\)内部，\(\gamma_1,\cdots,\gamma_n\)中的每一条都在其他\(n-1\)条的外部，\(D\)是由这\(n+1\)条曲线围成的域，用\(\gamma\)记\(D\)的边界，如果\(f\in H(D)\bigcap C(\bar D)\)，那么

\[\int_\gamma f(z)dz = 0 \]

或者也可以写作

\[\int_{\gamma_0} f(z)dz = \int_{\gamma_1} f(z)dz+\cdots+\int_{\gamma_n} f(z)dz \]

全纯函数的原函数

定义1

设\(f:D\to \bm C\)是定义在域\(D\)上的一个函数，如果存在\(F\in H(D)\)，使得\(F'(z)=f(z)\)在\(D\)上成立，就称\(F\)是\(f\)的一个原函数

定理1

设\(f\)在\(D\)中连续，且对\(D\)中任意可求长闭曲线\(\gamma\)均有

\[\int_\gamma f(z)dz=0 \]

那么

\[F(z) = \int^z_{z_0}f(\zeta)d\zeta \]

是\(D\)中的全纯函数，且在\(D\)中有\(F'(z)=f(z)\)，这里\(z_0\)是\(D\)中一固定点。

定理2

设\(D\)是\(\bm C\)中的单连通域，\(f\in H(D)\)，那么\(F(z)=\int^z_{z_0}f(\zeta)d\zeta\)是\(f\)在\(D\)中的一个原函数。

定理3

设\(D\)是\(\bm C\)中的单连通域，\(f\in H(D)\)，\(\varPhi\)是\(f\)的任一原函数，那么

\[\int^z_{z_0}f(\zeta)d\zeta = \varPhi(z)-\varPhi(z_0) \]

Cauchy积分公式

定理1

设\(D\)是由可求长简单闭曲线\(\gamma\)围成的域，如果\(f\in H(D)\bigcap C(\bar D)\)，那么对任意\(z\in D\)，均有

\[f(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(\zeta)}{\zeta-z}d\zeta \]

定理2

设\(\gamma\)是\(C\)中的可求长曲线，\(g\)是\(\gamma\)上的连续函数，那么由Cauchy型积分确定的函数

\[G(z) = \frac{1}{2\pi i}\int_\gamma \frac{g(\zeta)}{\zeta-z}d\zeta \]

在\(C\setminus y\)（差集）上有任意阶导数，而且

\[G^{(n)}(z)=\frac{n!}{2\pi i}\int_\gamma\frac{g(\zeta)}{(\zeta-z)^{n+1}}d\zeta,n=1,2,\cdots \]

定理3

设\(D\)是由可求长简单闭曲线\(\gamma\)围成的域，如果\(f\in H(D)\bigcap C(\bar D)\)，那么\(f\)在\(D\)上有任意阶导数，而且对任意\(z\in D\)，有

\[f^{(n)}(z)=\frac{n!}{2\pi i}\int_\gamma\frac{f(\zeta)}{(\zeta-z)^{n+1}}d\zeta,n=1,2,\cdots \]

定理4

如果\(f\)是域\(D\)上的全纯函数，那么\(f\)在\(D\)上有任意阶导数。

定理5

设\(\gamma_0,\gamma_1,\cdots,\gamma_k\)是\(k+1\)条可求长简单闭曲线，\(\gamma_1,\cdots,\gamma_k\)都在\(\gamma_0\)的内部，\(\gamma_1,\cdots,\gamma_k\)中的每一条都在其他\(k-1\)条的外部，\(D\)是由这\(k+1\)条曲线围成的域，\(D\)的边界\(\gamma\)由\(\gamma_0,\gamma_1,\cdots,\gamma_k\)所组成，如果\(f\in H(D)\bigcap C(\bar D)\)，则对任意\(z\in D\)，有

\[f(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(\zeta)}{\zeta-z}d\zeta \]

\(f\)在\(D\)内有任意阶导数，且

\[f^{(n)}(z)=\frac{n!}{2\pi i}\int_\gamma\frac{f(\zeta)}{(\zeta-z)^{n+1}}d\zeta,n=1,2,\cdots \]

Cauchy积分公式的一些重要推论

Cauchy不等式

设\(f\)在\(B(a,R)\)中全纯，且对任意\(z\in B(a,R)\)，有\(|f(z)|\leq M\)，那么

\[|f^{(n)}(a)|\leq\frac{n!M}{R^n},n=1,2,\cdots \]

Liouville定理

有界整函数必为常数

代数学基本定理

任意复系数多项式

\[P(z)=a_0z^n+a_1z^{n-1}+\cdots+a_n,a_0\neq 0 \]

在\(\bm C\)中必有零点

Morera定理

如果\(f\)是域\(D\)上的连续函数，且沿\(D\)内任一可求长闭曲线的积分为零，那么\(f\)在\(D\)上全纯

非齐次Cauchy积分公式

TODO

一维\(\bar\partial\)问题的解

TODO

全纯函数的Taylor展开及其应用

Weierstrass定理

设\(z_1,z_2,\cdots\)是\(\bm C\)中的一列复数，称

\[\sum^\infty_{n=1}z_n = z_1+z_2+\cdots \]

为一个复数项级数。这个级数称为是收敛的，如果它的部分和数列\(S_n=\sum^n_{k=1}z_k\)收敛，如果\(\{S_n\}\)的极限为\(S\)，就说这个级数的和为\(S\)，记为\(\sum^\infty_{n=1}z_n = S\)

从数列的Cauchy收敛准则马上可得级数的Cauchy收敛准则：

级数收敛的充要条件是对任意\(\varepsilon>0\)，存在正整数\(N\)，使得当\(n>N\)时，不等式

\[z_{n+1}+z_{n+2}+\cdots+z_{n+p}<\varepsilon \]

对任意自然数\(p\)成立

从收敛准则即得\(\sum^\infty_{n=1}z_n\)收敛的必要条件是\(\lim_{n\to \infty}z_n=0\)

如果\(\sum^\infty_{n=1}|z_n|\)收敛，就说级数\(\sum^\infty_{n=1}z_n\)绝对收敛。同样，绝对收敛的级数一定收敛，反之不一定成立。并且有\(\sum^\infty_{n=1}|z_n|\geq|\sum^\infty_{n=1}z_n|\)

另外，\(\sum^\infty_{n=1}z_n\)收敛的充要条件是其实部和虚部构成的数列分别都收敛。

设\(E\)是\(\bm C\)中的一个点集，\(f_n:E\to \bm C\)是定义在\(E\)上的一个函数列，如果对于每一个\(z\in E\)，级数

\[\sum^\infty_{n=1}f_n(z)=f_1(z)+f_2(z)+\cdots \]

收敛到\(f(z)\)，就说其在\(E\)上收敛，其和函数为\(f\)，记为\(\sum^\infty_{n=1}f_n(z)=f(z)\)

一致连续

设\(\sum^\infty_{n=1}f_n(z)\)是定义在点集\(E\)上的级数，我们说\(\sum^\infty_{n=1}f_n(z)\)在\(E\)上一致收敛到\(f(z)\)，是指对任意\(\varepsilon>0\)，存在正整数\(N\)，当\(n>N\)时，不等式

\[|S_n(z)-f(z)|<\varepsilon \]

对所有的\(z\in E\)成立，这里，\(S_n(z)=\sum^n_{k=1}f_k(z)\)是级数的部分和。

Cauchy收敛准则

级数\(\sum^\infty_{n=1}f_n(z)\)在\(E\)上一致收敛的充要条件是对任意\(\varepsilon>0\)，存在正整数\(N\)，当\(n>N\)时，不等式

\[|f_{n+1}(z)+f_{n+2}(z)+\cdots+f_{n+p}(z)|<\varepsilon \]

对所有\(z\in E\)及任意自然数\(p\)成立。

Weierstrass一致收敛判别法

设\(f_n:E\to \bm C\)是定义在\(E\)上的函数列，且在\(E\)上满足\(|f_n(z)|\leq a_n,n=1,2,\cdots\)，如果\(\sum^\infty_{n=1}a_n\)收敛，那么\(\sum^\infty_{n=1}f_n(z)\)在\(E\)上一致收敛。

定理1

设级数\(\sum^\infty_{n=1}f_n(z)\)在点集\(E\)上一致收敛到\(f(z)\)，如果每个\(f_n(n=1,2,\cdots)\)都是\(E\)上的连续函数，那么\(f\)也是\(E\)上的连续函数。

定理2

设级数\(\sum^\infty_{n=1}f_n(z)\)在可求长曲线\(\gamma\)上一致收敛到\(f(z)\)，如果每个\(f_n(n=1,2,\cdots)\)都在\(\gamma\)上连续，那么

\[\int_\gamma f(z)dz=\sum^\infty_{n=1}\int_\gamma f_n(z)dz \]

内闭一致收敛

如果级数\(\sum^\infty_{n=1}f_n(z)\)在域\(D\)的任意紧子集上一致收敛，就称\(\sum^\infty_{n=1}f_n(z)\)在\(D\)中内闭一致收敛。

定义1

如果\(D\)的子集\(G\)满足

\(\bar G\subset D\)
\(\bar G\)是紧的

就说\(G\)相对于\(D\)是紧的，记为\(G\subset\subset D\)

引理1

设\(D\)是\(\bm C\)中的域，\(K\)是\(D\)中的紧子集，且包含在相对于\(D\)是紧的开集\(G\)中，即\(K\subset G\subset\subset D\)，那么对任意\(f\in H(D)\)，均有

\[sup\{|f^{(k)}|:z\in K\}\leq Csup{|f(z)|:z\in G} \]

这里，\(k\)是任意自然数，\(C\)是与\(k,K,G\)有关的常数。

Weierstrass定理

设\(D\)是\(\bm C\)中的域，如果

\(f_n\in H(D),n=1,2,\cdots\)
\(\sum^\infty_{n=1} f_n(z)\)在\(D\)中内闭一致收敛到\(f(z)\)

那么

\(f\in H(D)\)
对任意自然数\(k\)，\(\sum^\infty_{n=1} f_n^{(k)}(z)\)在\(D\)中内闭一致收敛到\(f^{(k)}(z)\)

幂级数

幂级数，是指形如

\[\sum^\infty_{n=0}a_n(z-z_0)^n = a_0+a_1(z-z_0)+a_2(z-z_0)^2+\cdots \]

的级数，其中\(a_n,z_0\)都是复常数。

定义1

如果存在常数\(R\)，使得当\(|z|< R\)时，级数\(\sum^\infty_{n=0}a_nz^n\)收敛；当\(|z|>R\)时，级数发散，就称\(R\)为该级数的收敛半径，\(\{z:|z|< R\}\)称为该级数的收敛圈。

定理1

\(\sum^\infty_{n=0}a_nz^n\)的收敛半径为

\[R=1\bigg/\overline{\lim_{n\to\infty}}\sqrt[n]{|a_n|} \]

其中\(\overline\lim\)是上极限

Abel定理

如果\(\sum^\infty_{n=0}a_nz^n\)在\(z=z_0\neq 0\)处收敛，则必在\(\{z:|z|<|z_0|\}\)中内闭绝对一致收敛。

定理2

幂级数在其收敛圆内确定一个全纯函数。

非切向极限

设\(g\)是定义在单位圆中的函数，\(e^{i\theta_0}\)是单位圆周上一点，\(S_\alpha(e^{i\theta_0})\)如下图所示，其中\(\alpha<\frac{\pi}{2}\)，如果当\(z\)在\(S_\alpha(e^{i\theta_0})\)中趋于\(e^{i\theta_0}\)时，\(g(z)\)有极限\(l\)，就称\(g\)在\(e^{i\theta_0}\)处有非切向极限\(l\)，记为

\[\lim_{z\to e^{i\theta_0},z\in S_\alpha(e^{i\theta_0})}g(z)=l \]

Abel第二定理

设\(f(z)=\sum^\infty_{n=0}a_nz^n\)的收敛半径\(R=1\)，且级数在\(z=1\)处收敛于\(S\)，那么\(f\)在\(z=1\)处有非切向极限\(S\)，即

\[\lim_{z\to 1,z\in S_\alpha(1)}f(z)=S \]

其他一些求收敛半径的方法

总体上和高等数学差别不大

比值法

如果\(\lim_{n\to \infty}|c_{n+1}/c_n|=\lambda\neq 0\)，那么半径为\(R=1/\lambda\)

根值法

如果\(\lim_{n\to \infty}\sqrt[n]{|c_n|}=\mu\neq 0\)，那么半径为\(R=1/\mu\)

定理3

设幂级数\(\sum^\infty_{n=0}c_n(z-z_0)^n\)的收敛半径为\(R\)，那么

它的和函数\(f(z)\)，即

\[f(z) = \sum^\infty_{n=0}c_n(z-a)^n \]

是收敛圆：\(|z-a|< R\)内的解析函数

\(f(z)\)在收敛圆内的导数可将其幂级数逐项求导得到，即

\[f'(z) = \sum^\infty_{n=0}nc_n(z-a)^{n-1} \]

\(f(z)\)在收敛圆内可以逐项积分，即

\[\int_C f(z)dz = \sum^\infty_{n=0}c_n\int_C(z-a)^ndz, C\in|z-a|< R \]

或

\[\int_0^zf(z)dz = \sum^\infty_{n=0}\frac{c_n}{n+1}(z-a)^{n+1} \]

全纯函数的Taylor展开

前面已经证明，幂级数在它的收敛圆内表示一个全纯函数，而在一个圆内全纯的函数也一定可以展开成幂级数。

定理1

若\(f\in H(B(z_0,R))\)，则\(f\)可以在\(B(z_0,R)\)中展开成幂级数

\[f(z)=\sum_{n=0}^\infty\frac{f^{(n)}(z_0)}{n!}(z-z_0)^n,z\in B(z_0,R) \]

右端的级数称为\(f\)的Taylor级数

定理2

\(f\)在点\(z_0\)处全纯的充要条件是\(f\)在\(z_0\)的邻域内可以展开成幂级数

\[f(z)=\sum_{n=0}^\infty a_n(z-z_0)^n \]

定义1

设\(f\)在\(z_0\)点全纯且不恒为零，如果

\[f(z_0)=0,f'(z_0)=0,\cdots,f^{(m-1)}(z_0)=0,f^{(m)}(z_0)\neq 0 \]

则称\(z_0\)是\(f\)的\(m\)阶零点。

命题1

\(z_0\)为\(f\)的\(m\)阶零点的充要条件是\(f\)在\(z_0\)的邻域内可以表示为

\[f(z)=(z-z_0)^mg(z) \]

这里，\(g\)在\(z_0\)点全纯，且\(g(z_0)\neq 0\)

事实上，如果\(z_0\)是\(f(z)\)的\(m\)阶零点，那么\(f(z)\)可以表示成上述的形式，设\(g(z)\)在\(z_0\)处的泰勒展开为

\[g(z) = c_0+c_1(z-z_0)+c_2(z-z_0)^2+\cdots \]

其中\(c_0=g(z_0)\neq 0\)，从而

\[f(z) = c_0(z-z_0)^m+c_1(z-z_0)^{m+1}+\cdots \]

也就是前\(m\)项系数都为0.

命题2

设\(D\)是\(\bm C\)中的域，\(f\in H(D)\)，如果\(f\)在\(D\)中的小圆盘\(B(z_0,\varepsilon)\)上恒等于零，那么\(f\)在\(D\)上恒等于\(0\)。

命题3

设\(D\)是\(\bm C\)中的域，\(f\in H(D), f(z)\not\equiv 0\)，那么\(f\)在\(D\)中的零点是孤立的。即若\(z_0\)为\(f\)的零点，则必存在\(z_0\)的领域\(B(z_0,\varepsilon)\)，使得\(f\)在\(B(z_0,\varepsilon)\)中除了\(z_0\)外不再有其他的零点。

唯一性定理

设\(D\)是\(\bm C\)中的域，\(f_1,f_2\in H(D)\)，如果存在\(D\)中的点列\(\{z_n\}\)，使得\(f_1(z_n)=f_2(z_n),n=1,2,\cdots\)，且\(\lim_{n\to\infty}z_n=a\in D\)，那么在\(D\)中有\(f_1(z)=\equiv f_2(z)\)

常见的泰勒展开

以下都是在\(z=0\)处的展开式

\[\frac{1}{1-z}=\sum^\infty_{n=0}z^n,|z|<1 \]

\[\frac{1}{1+z}=\sum^\infty_{n=0}(-1)^nz^n,|z|<1 \]

\[e^z = \sum^\infty_{n=0} \frac{z^n}{n!},z\in\bm C \]

\[cosz = \sum^\infty_{n=0} (-1)^n\frac{z^{2n}}{(2n)!},z\in\bm C \]

\[sinz = \sum^\infty_{n=0} (-1)^n\frac{z^{2n+1}}{(2n+1)!},z\in\bm C \]

\[\log(1+z) = \sum^\infty_{n=1} (-1)^{n-1}\frac{z^n}{n},|z|<1 \]

\[exp[a\log(1+z)] = \sum^\infty_{n=0}\binom{a}{n}z^n,|z|<1 \]

辐角原理和Rouche定理

TODO

最大模原理和Schwarz引理

TODO

全纯函数的Laurent展开及其应用

前面证明了，圆盘中的全纯函数一定可以在圆盘中展开成幂级数。但圆环中的全纯函数不一定，但是一定可以展开成洛朗级数。

全纯函数的Laurent展开

称级数

\[\sum^\infty_{n=-\infty}a_n(z-z_0)^n=\sum^\infty_{n=0}a_n(z-z_0)^n+\sum^\infty_{n=1}a_{-n}(z-z_0)^{-n} \]

为洛朗级数。由两部分组成，第一部分是幂级数，第二部分为负幂项的级数。如果这两个级数都收敛，则整个洛朗级数收敛。

定理1

如果洛朗级数

\[\sum^\infty_{n=-\infty}a_n(z-z_0)^n=\sum^\infty_{n=0}a_n(z-z_0)^n+\sum^\infty_{n=1}a_{-n}(z-z_0)^{-n} \]

的收敛域为圆环\(D=\{z:r< |z-z_0|< R\}\)，那么它在\(D\)中绝对收敛且内闭一致收敛，它的和函数在\(D\)中全纯。

上述级数的幂级数部分称为全纯部分，负幂项级数部分称为主要部分。

该定理的逆定理也成立。

设\(D=\{z:r<|z-z_0|< R\}\)，如果\(f\in H(D)\)，那么\(f\)在\(D\)上可以展开为洛朗级数

\[f(z) = \sum^\infty_{n=-\infty}a_n(z-z_0)^n \]

其中

\[a_n = \frac{1}{2\pi i}\int_{\gamma_\rho}\frac{f(\zeta)}{(\zeta-z_0)^{n+1}}d\zeta \]

\[\gamma_\rho = \{\zeta:|\zeta-z_0|=\rho\}(r<\rho< R) \]

并且这个展开式是唯一的。

孤立奇点

如果\(f\)在无心圆盘\(\{z:0<|z-z_0|< R\}\)中全纯（而在圆心不全纯），就称\(z_0\)是\(f\)的孤立奇点。在奇点附近有三种情况

\(\lim_{z\to z_0}f(z)=a,a\)是一有限数，这时称\(z_0\)是\(f\)的可去奇点
\(\lim_{z\to z_0}f(z)=\infty\)，这时称\(z_0\)是\(f\)的极点
\(\lim_{z\to z_0}f(z)\)不存在，这时称\(z_0\)是\(f\)的本性奇点

定理1

\(z_0\)是\(f\)的可去奇点的充要条件是\(f\)在\(z_0\)附近有界。

命题1

\(z_0\)是\(f\)的极点的充要条件是\(z_0\)为\(1/f\)的零点。

定义1

如果\(z_0\)是\(1/f(z)\)的\(m\)阶零点，就称\(z_0\)是\(f\)的\(m\)阶极点。

定理2

\(z_0\)是\(f\)的\(m\)阶极点的充要条件是\(f\)在\(z_0\)附近的洛朗级数为

\[f(z) = \frac{a_{-m}}{(z-z_0)^m}+\cdots+\frac{a_{-1}}{z-z_0}+a_0+a_1(z-z_0)+\cdots \]

其中\(a_{-m}\neq 0\)

定理3

\(f\)在可去奇点处的特征是洛朗级数没有主要部分，只有全纯部分

\(f\)在极点处的特征是洛朗级数的主要部分只有有限项。最高负幂项为\(t^{-m}\)，则为\(m\)级极点。

\(f\)在本性奇点处的特征是洛朗级数的主要部分有无限项。

定理4

设\(z_0\)是\(f\)的本性奇点，那么对任意\(A\in\bm C_\infty\)，必存在趋于\(z_0\)的点列\(\{z_n\}\)，使得\(\lim_{n\to\infty}f(z_n)=A\)

定理5

全纯函数在本性奇点的邻域内无穷多次地取到每个有穷复值，最多只有一个例外

定义2

我们讨论无穷远点。如果\(f\)在无穷远点的邻域（不包括无穷远点）\(\{z:0\leq R<|z|<\infty\}\)中全纯，\(\infty\)就是\(f\)的孤立奇点。

记

\[g(\zeta)=f(\frac{1}{\zeta}) \]

如果\(\zeta=0\)是\(g\)的可去奇点、\(m\)阶极点或本性奇点，那么我们相应地称\(z=\dfrac{1}{\zeta}=\infty\)是\(f\)的可去奇点、\(m\)阶极点或本性奇点。

整函数与亚纯函数

如果\(f\)在整个复平面\(\bm C\)上全纯，就称\(f\)为整函数

定理1

在无穷远处全纯的整函数一定是常数。

定理2

如果无穷远点是整函数\(f\)的一个\(m\)阶极点，那么\(f\)是一个\(m\)次多项式。

如果\(f\)在整个复平面\(\bm C\)上除去极点外没有其他的奇点，就称\(f\)是一个亚纯函数。整函数显然是亚纯函数。

此外有理函数

\[f(z) = \frac{P_n(z)}{Q_m(z)} \]

也是亚纯函数，这里，\(P_n(z),Q_m(z)\)是两个既约（分式最简）的多项式

定理3

若\(z=\infty\)是亚纯函数\(f\)的可去奇点或极点，则\(f\)一定是有理函数。

反过来也成立。

残数定理

定义1

设\(a\)是\(f\)的一个孤立奇点，\(f\)在\(a\)点的邻域\(B(a,r)\)中的洛朗级数为\(f(z)=\sum^\infty_{n=-\infty}c_n(z-a)^n\)，称\(c_{-1}\)为\(f\)在\(a\)点的残数，记为

\[Res(f,a) = c_{-1} \]

或

\[\underset{z=a}{Res}f = c_{-1} \]

根据洛朗级数的计算方法，我们知道

\[c_{-1} = \frac{1}{2\pi i}\int_\gamma f(\zeta)d\zeta \]

结合上上式就有

\[\int_\gamma f(z)dz = 2\pi iRes(f,a) \]

这里，\(\gamma=\{z:|z-a|=\rho\},0<\rho< r\)

若\(z=\infty\)是\(f\)的孤立奇点，即\(f\)在\(R<|z|<\infty\)中全纯，我们定义\(f\)在\(z=\infty\)处的残数为

\[Res(f,\infty) = -\frac{1}{2\pi i}\int_\gamma f(z)dz \]

这里，\(\gamma=\{z:|z|=\rho\},R<\rho<\infty\)

命题1

若\(a\)是\(f\)的\(m\)阶极点，则

\[Res(f,a) = \frac{1}{(m-1)!}\lim_{z\to a}\frac{d^{m-1}}{dz^{m-1}}\{(z-a)^mf(z)\} \]

命题2

若\(a\)是\(f\)的\(1\)阶极点，则

\[Res(f,a) = \lim_{z\to a}(z-a)f(z) \]

命题3

设\(f=\frac{g}{h}\)，\(g,h\)都在\(a\)处全纯，且\(g(a)\neq 0\)，\(h(a)=0\)，\(h'(a)\neq 0\)，那么

\[Res(f,a) = \frac{g(a)}{h'(a)} \]

残数定理

设\(D\)是复平面上的一个有界区域，它的边界\(\gamma\)由一条或若干条简单闭曲线组成，如果\(f\)在\(D\)中除去孤立奇点\(z_1,\cdots,z_n\)外是全纯的，在闭域\(\overline{D}\)上除去\(z_1,\cdots,z_n\)外是连续的，那么

\[\int_\gamma f(z)dz = 2\pi i\sum^n_{k=1} Res(f,z_k) \]

定理1

若\(f\)在\(\bm C\)中除去\(z_1,\cdots,z_n\)外是全纯的，则\(f\)在\(z_1,\cdots,z_n\)及\(z=\infty\)处的残数之和为零。

这个定理可以用在，在用残数定理求积分时，如果里面的众多奇点不好算，就可以转化为算无穷远点的残数来代替。

定理2

\[Res[f(z),\infty] = -Res\bigg[f\bigg(\frac{1}{z}\bigg)\cdot\frac{1}{z^2},0\bigg] \]

利用残数定理计算定积分

\(\int^\infty_{-\infty}f(x)dx\)型

设\(f\)在上半平面\(\{z: Imz>0\}\)中除去\(a_1,\cdots,a_n\)外是全纯的，在\(\{z: Imz\geq0\}\)中除去\(a_1,\cdots,a_n\)外是连续的，如果\(\lim_{z\to\infty}zf(z)=0\)，那么

\[\int^\infty_{-\infty}f(x)dx = 2\pi i\sum^n_{k=1}Res(f,a_k) \]

推论1

设\(P,Q\)是两个既约多项式，\(Q\)没有实的零点，且\(degQ-degP\geq2\)，那么

\[int^\infty_{-\infty}\frac{P(x)}{Q(x)}dx = 2\pi i\sum^n_{k=1}Res\bigg(\frac{P(z)}{Q(z)},a_k\bigg) \]

这里\(a_k\)为\(Q\)在上半平面中的全部零点，\(degP,degQ\)为\(P,Q\)的次数。

Jordan引理

设\(f\)在\(\{z:R_0\leq|z|<\infty,Imz\geq0\}\)上连续，且\(\lim_{z\to\infty,Imz\geq0}f(z)=0\)，则对任意\(a>0\)，有

\[\lim_{R\to\infty}\int_{\gamma_R}e^{iaz}f(z)dz = 0 \]

这里\(\gamma_R=\{z:z=Re^{i\theta},0\leq\theta\leq\pi,R\geq R_0\}\)

定理1

设\(f\)在上半平面\(\{z: Imz>0\}\)中除去\(a_1,\cdots,a_n\)外是全纯的，在\(\{z: Imz\geq0\}\)中除去\(a_1,\cdots,a_n\)外是连续的，如果\(\lim_{z\to\infty}f(z)=0\)，那么对任意\(\alpha>0\)，有

\[\int^\infty_{-\infty}e^{i\alpha x}f(x)dx = 2\pi i\sum^n_{k=1}Res(e^{i\alpha z}f(z),a_k) \]

推论2

\[\int^\infty_{-\infty}f(x)\cos\alpha xdx = Re\{ 2\pi i\sum^n_{k=1}Res(e^{i\alpha z}f(z),a_k) \} \]

\[\int^\infty_{-\infty}f(x)\sin\alpha xdx = Im\{ 2\pi i\sum^n_{k=1}Res(e^{i\alpha z}f(z),a_k) \} \]

引理1

设\(f\)在扇形域

\[G = \{z=a+\rho e^{i\theta}:0<\rho\leq \rho_0,\theta_0\leq\theta\leq\theta_0+\alpha\} \]

上连续，如果\(\lim_{z\to a}(z-a)f(z) = A\)，那么

\[\lim_{\rho\to 0}\int_{\gamma_\rho}f(z)dz = iA\alpha \]

这里，\(\gamma_\rho = \{z=a+\rho e^{i\theta}:\theta_0\leq\theta\leq\theta_0+\alpha\}\)，它的方向是沿着辐角增加的方向。

\(\int^\infty_0f(x)dx\)型

TODO

\(\int^b_af(x)dx\)型

对于一种重要的又穷限积分

\[\int^{2\pi}_0 R(\sin\theta,\cos\theta)d\theta \]

一种办法是

\[\int^{2\pi}_0 R(\sin\theta,\cos\theta)d\theta = 2\int^\infty_{-\infty}R\bigg(\frac{2t}{1+t^2},\frac{1-t^2}{1+t^2}\bigg)\frac{1}{1+t^2}dt \]

另一种办法是

\[\int^{2\pi}_0 R(\sin\theta,\cos\theta)d\theta = \int_{|z|=1}R\bigg(\frac{1}{2i}\bigg(z-\frac{1}{z}\bigg),\frac{1}{2}\bigg(z+\frac{1}{z}\bigg)\bigg)\frac{1}{iz}dz \]

对于另一种重要的又穷限积分

\[\int^b_a(x-a)^r(b-x)^sf(x)dx \]

TODO

Fresnel积分

\[\int^\infty_0 \cos x^2dx = \int^\infty_0 \sin x^2dx = \frac{1}{2}\sqrt{\frac{\pi}{2}} \]

Poisson积分

\[\int^\infty_0 e^{-ax^2}\cos bxdx = \frac{1}{2}\sqrt{\frac{\pi}{a}}exp\bigg(-\frac{b^2}{4a}\bigg) \]

共形映射

分式线性变换

见前

几个初等函数所构成的映射

幂函数

\(\omega=z^n(n\in N,n\geq2)\)这个函数在\(z\)平面内处处可导，当\(z\neq 0\)时\(\omega'\neq 0\)，也就是说除了原点外处处共形映射。

幂函数映射的特点是：把以原点为顶点的角形域映射为以原点为顶点的角形域。但张角变成了原来的\(n\)倍。

指数函数

\(\omega=e^z\)，易知在全平面上都是一个共形映射。

其特点是：把水平的带形区域\(0< Im(z)< a(a\leq 2\pi)\)映射成角形域\(0< arg\omega< a\)。

几个常见的分式线性变换

把单位圆映为单位圆

\[w = e^{i\varphi}\bigg(\dfrac{z-\alpha}{1-\bar{\alpha}z}\bigg),|\alpha|<1,\varphi\in R \]

把上半平面映为单位圆

\[w = e^{i\theta}\bigg(\dfrac{z-\lambda}{z-\bar{\lambda}}\bigg),Im(\lambda)>0,\theta\in R \]