有两种方法描述几何:隐式的、显式的。
几何的隐式表示
取决于某些点是否符合表达式。
例如描述一个球面\(x^2+y^2+z^2=1\),所有符合这个表达式的点就是一个球面。
更一般的情况:满足\(f(x,y,z)=0\)的所有点。
它的特点是,采样比较困难,但判断一个点在集合体内外或者在几何体上非常方便。
隐式表示包含:
- 代数方程表示(Algebraic Surfaces)
- 通过布尔表达式对几何体进行运算(Constructive Solid Geometry)
- 距离函数(Distance Functions)
- Blending Distance Functions
- 水平集(Level Set)
- 分形(Fractals)
几何的显式表示
所有的点直接给出,或者通过参数映射地给出。
比如从二维映射到三维
\[f:\mathbb{R^2\to R^3};(u,v)\to(x,y,z) \]
特点是,采样简单,但是判断关系较为困难。
显式表示包含:
- 点云(Point Cloud)
- 多边形网格(Polygon Mesh)
- 贝赛尔曲线(Bezier Curves)
贝塞尔曲线
Casteljau算法
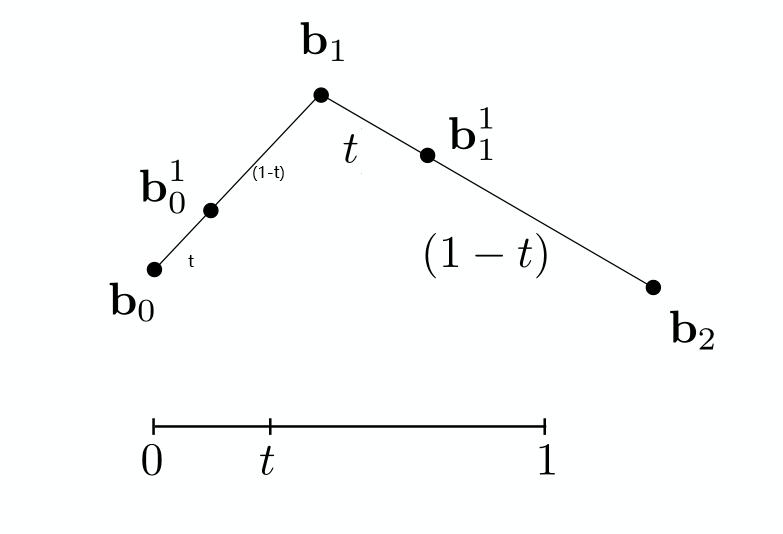
考虑平面上的三个点\(b_0,b_1,b_2\),用线性差值的办法插入一个点到每一条边上。
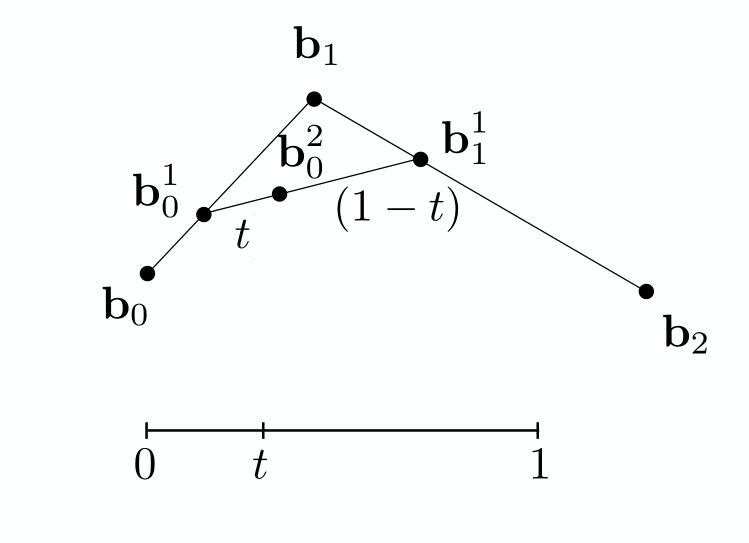
将新增的两个点再利用相同的办法插入一个点。
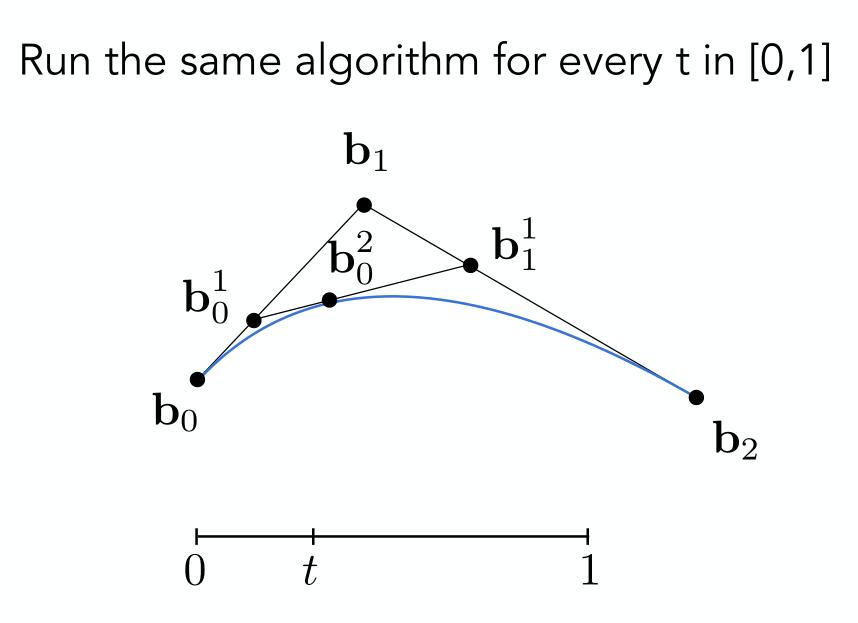
然后对于插值的比例值\([0,1]\)上的所有点进行这个算法。
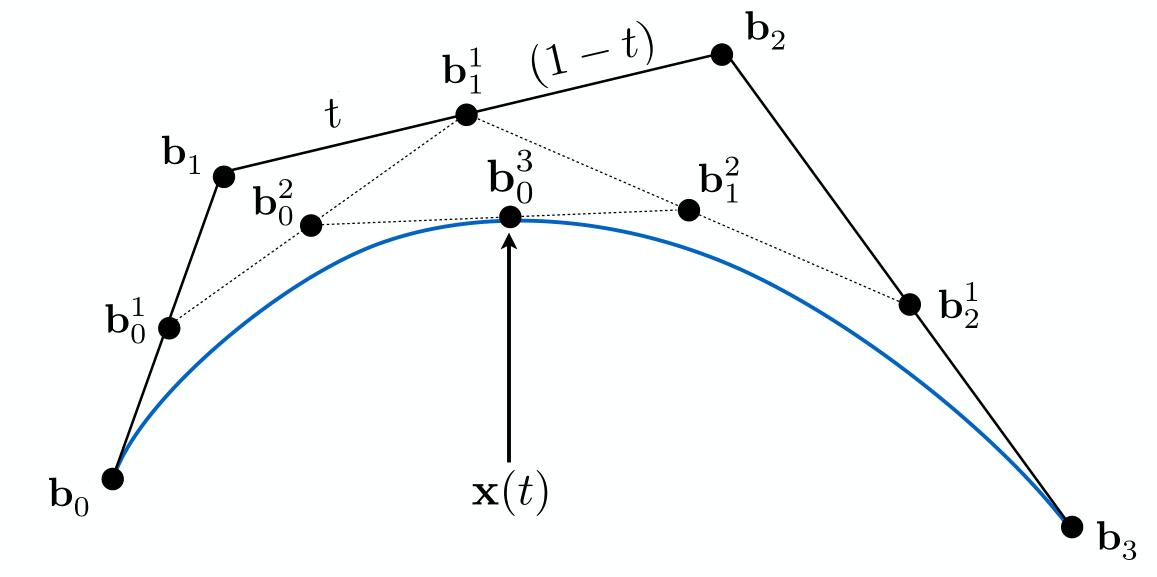
对于更多点,因为每次在边上进行插值后,新的点比原来的点少一个,反复进行这个算法直到只有一个点。
将这个过程公式化,对于三个点的情况,即为
\[b_0^1(t)=(1-t)b_0+tb_1\\ b_1^1(t)=(1-t)b_1+tb_2\\ b_0^2(t)=(1-t)b_0^1+tb_1^1 \]
\[\therefore b_0^2(t) = (1-t)^2b_0+2t(1-t)b_1+t^2b_2 \]
对于更多点的情况:
\[b^n(t) = b^n_0(t)=\sum^n_{j=0}b_jB^n_j(t) \]
其中
\[B^n_i(t)=\binom{n}{i}t^i(1-t)^{n-1} \]
也可以用递归的方法计算,比较简便。
贝赛尔曲线的一些性质
- \(t=0\)是起点,\(t=1\)是终点。
- 曲线与端点段相切
- 仿射变换中,对控制点仿射变换再画曲线,和对已经画出来的曲线做仿射变换,得到的曲线是一样的。
- 曲线一定在控制点的凸包内
分段的贝赛尔曲线及其算法
四个顶点构成的贝赛尔曲线为一段,再将许多贝赛尔曲线接到一起。
这样的曲线一定是连续的,但光滑还有一个条件。即第一条曲线的第3、4个点的线段和第二条曲线的第1、2个点的线段长度、方向均相同。
样条(Spline)
TODO
贝塞尔曲面
对于\(4\times 4\)的控制点,首先在\(u\)方向上画出四条贝赛尔曲线,然后再在\(v\)方向上,根据四条贝塞尔曲线计算出四个控制点,再计算出曲面上的点。